题目内容

4．△ABC中，内角A、B、C所对的边分别为a、b、c，且acosB-bcosA=$\frac{1}{2}$c，则$\frac{tanA}{tanB}$=3．

分析 由题意和正弦定理以及和差角的三角函数公式可得sinAcosB=3sinBcosA，由同角三角函数基本关系整体代入可得．

解答 解：∵△ABC中acosB-bcosA=$\frac{1}{2}$c，
∴由正弦定理可得sinAcosB-sinBcosA=$\frac{1}{2}$sinC，
∴2sinAcosB-2sinBcosA=sinC=sin（A+B），
∴2sinAcosB-2sinBcosA=sinAcosB+sinBcosA，
∴sinAcosB=3sinBcosA，
∴$\frac{tanA}{tanB}$=$\frac{sinAcosB}{cosAsinB}$=3，
故答案为：3．

点评 本题考查正弦定理解三角形，涉及和差角的三角函数公式以及同角三角函数基本关系，属基础题．

练习册系列答案
相关题目
3．某几何体的三视图如图所示，则该几何体的外接球的体积为（　　）
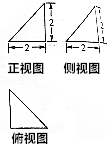
A．12πB．4$\sqrt{3}$πC．48πD．32$\sqrt{3}π$
4．已知等差数列2，a2，a3，8，a5的公差是d1，等差数列-4，b2，b3，b4，12，b6的公差是d2，求$\frac{{d}_{1}}{{d}_{2}}$的值．
12．为了得到函数y=3sin$\frac{x}{3}$的图象，只需把函数y=sinx图象上所有的点的（　　）
A．横坐标伸长到原来的3倍，纵坐标变为原来的3倍
B．横坐标缩小到原来的$\frac{1}{3}$倍，纵坐标变为原来的$\frac{1}{3}$倍
C．横坐标伸长到原来的$\frac{1}{3}$倍，纵坐标变为原来的3倍
D．横坐标伸长到原来的3倍，纵坐标变为原来的$\frac{1}{3}$倍
19．已知角θ的顶点在平面直角坐标系xOy原点O，始边为x轴正半轴，终边在直线x-2y=0上，则sin2θ=（　　）
A．$\frac{4}{5}$B．-$\frac{4}{5}$C．$\frac{3}{5}$D．-$\frac{3}{5}$
9．若$\frac{cos2α}{sin（α+\frac{π}{4}）}$=-$\frac{2\sqrt{5}}{5}$，且α∈（$\frac{π}{4}$，$\frac{π}{2}$），则tan2α的值是（　　）
A．-$\frac{4}{3}$B．-$\frac{3}{4}$C．$\frac{3}{4}$D．$\frac{4}{3}$
16．下列说法正确的是（　　）
A．命题“p或q”为真命题，则命题p和命题q均为真命题
B．命题“已知A、B为一个三角形的两内角，若A＞B，则sinA＞sinB”的逆命题为真命题
C．“若a＞b，则2a＞2b-1”的否命题为“若a＜b，则2a＜2b-1”
D．“a=1”是“直线x-ay+1=0与直线x+ay-2=0互相垂直”的充要条件．
13．计算：cos25°sin55°-cos65°cos55°=（　　）
A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．$\frac{\sqrt{3}}{2}$D．-$\frac{\sqrt{3}}{2}$
14．已知A（0，-5），B（0，-1），则以线段AB为直径的圆的方程是（　　）
A．（x+3）2+y2=2B．x2+（y+3）2=4C．（x+3）2+y2=2D．（x-3）2+y2=4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网