Question

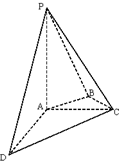如图在四棱锥P-ABCD中，PA丄平面ABCD，AC丄AD，AB丄BC，∠BAC=45°，PA=AD=2，AC=1．建立适当的空间直角坐标系，利用空间向量方法解答以下问题：
（Ⅰ）证明：PC⊥AD；
（Ⅱ）求二面角A-PC-D的余弦值；
（Ⅲ）设E为棱PA上的点，满足异面直线BE与CD所成的角为30°，求AE的长．

Answer 1

考点：与二面角有关的立体几何综合题,空间中直线与直线之间的位置关系

专题：空间位置关系与距离,空间角

分析：（I）以

AD

，

AC

，

AP

为x，y，z正半轴方向，建立空间直角坐标系A-xyz，求出PC与AD的方向向量，根据两向量数量积为0，可得PC⊥AD；
（Ⅱ）求出平面PCD和平面PAC的法向量，代入向量夹角公式，可得二面角A-PC-D的余弦值；
（Ⅲ）由E为棱PA上的点，设AE=h∈[0，2]；结合异面直线BE与CD所成的角为30°，构造关于h的方程，解方程可得AE的长．

解答： 证明：（I）∵PA丄平面ABCD，AC丄AD，
∴以

AD

，

AC

，

AP

为x，y，z正半轴方向，建立空间直角坐标系A-xyz，
又∵AB丄BC，∠BAC=45°，PA=AD=2，AC=1．
D（2，0，0），C（0，1，0），B（-

1

2

，

1

2

，0），P（0，0，2），
∴

PC

=（0，1，-2），

AD

=（2，0，0），
∵

PC

•

AD

=0，
∴

PC

⊥

AD

．
解：（II）∵

PC

=（0，1，-2），

CD

=（2，-1，0），
设平面PCD的法向量

m

=（x，y，z）．
则

m • PC =0 m • CD =0

，即

y-2z=0 2x-y=0

，
令z=1，则

m

=（1，2，1），
又∵

AD

为平面PAC的法向量，
∴二面角A-PC-D的平面角θ满足：
cosθ=

| AD • m |

| AD |•| m |

=

6

6

，
即二面角A-PC-D的余弦值

6

6

．…（8分）
（III）设AE=h∈[0，2]；则

AE

=(0，0，h)，

BE

=(

1

2

，-

1

2

，h)，

CD

=(2，-1，0)，
又异面直线BE与CD所成的角为30°，
∴

| BE • CD |

| BE |•| CD |

=

3

10+20h2

=cos30°=

3

2

，
解得：h=

10

10

即AE=

10

10

．    …（12分）

点评：本题考查的知识点是向量法证明线线垂直，求二面角，及异面直线的夹角，建立空间坐标系是解答的关键．