��Ŀ����
Ϊ�˵����ѧ���������Ƿ�Ӱ��ѧϰ�Ŀ�����ѯ���˴�ѧһ�����꼶��200����ѧ����ѯ�ʵĽ����¼���£����д�ѧһ�꼶110��ѧ������45����Ϊ����Ӱ��ѧϰ����65����Ϊ��Ӱ��ѧϰ����ѧ���꼶90��ѧ������55����Ϊ����Ӱ��ѧϰ����35����Ϊ��Ӱ��ѧϰ��
��1�������������ݻ���һ��2��2����������
��2���ݴ˻ش��ܷ���99%�İ��ն϶���ѧ�����꼶��ͬ��������������̬��Ҳ��ͬ��
������
��1�������������ݻ���һ��2��2����������
��2���ݴ˻ش��ܷ���99%�İ��ն϶���ѧ�����꼶��ͬ��������������̬��Ҳ��ͬ��
������
| p��K2��k0�� | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.789 | 10.828 |
���㣺�����Լ����Ӧ��
ר�⣺�ۺ���,������ͳ��
��������1���������д�ѧһ�꼶110��ѧ������45����Ϊ����Ӱ��ѧϰ����65����Ϊ��Ӱ��ѧϰ����ѧ���꼶90��ѧ������55����Ϊ����Ӱ��ѧϰ����35����Ϊ��Ӱ��ѧϰ���ɵ�2��2����������
��2����K2ͳ��������ѧ��ʽ���㣬���ٽ�ֵ�Ƚϣ����ɵó����ۣ�
��2����K2ͳ��������ѧ��ʽ���㣬���ٽ�ֵ�Ƚϣ����ɵó����ۣ�
���
�⣺��1��2��2��������Ϊ��
��2����K2ͳ��������ѧ��ʽ�ã�k=
=
��8.08��6.635
����99%�İ���˵����ѧ�����꼶��ͬ��������������̬��Ҳ��ͬ��
| ��Ӱ�� | ��Ӱ�� | �ϼ� | |
| ��һ | 45 | 65 | 110 |
| ��� | 55 | 35 | 90 |
| �ϼ� | 100 | 100 | 200 |
| 200(45��35-55��65)2 |
| 100��100��110��90 |
| 800 |
| 99 |
����99%�İ���˵����ѧ�����꼶��ͬ��������������̬��Ҳ��ͬ��
���������⿼������Լ����Ӧ�ã�����ѧ���ļ�������������K2ͳ���������ٽ�ֵ�Ƚ��ǹؼ���

��ϰ��ϵ�д�
 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д� ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д�
�����Ŀ
��f��x����R�ϵ��溯������2f��0����ֵ���ڣ�������
| A��0 | B��1 | C��2 | D��4 |
��֪
=-2����tanx��ֵΪ��������
| 1-cosx+sinx |
| 1+cosx+sinx |
A��
| ||
B��-
| ||
C��
| ||
D��-
|
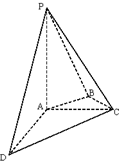 ��ͼ������P-ABCD�У�PA�Aƽ��ABCD��AC�AAD��AB�ABC����BAC=45�㣬PA=AD=2��AC=1�������ʵ��Ŀռ�ֱ������ϵ�����ÿռ�������������������⣺
��ͼ������P-ABCD�У�PA�Aƽ��ABCD��AC�AAD��AB�ABC����BAC=45�㣬PA=AD=2��AC=1�������ʵ��Ŀռ�ֱ������ϵ�����ÿռ�������������������⣺