题目内容
(1+x)(1-x)(2-x)5的展开式含x2项的系数是( )
| A、-80 | B、48 | C、80 | D、78 |
考点:二项式系数的性质
专题:二项式定理
分析:把所给的式子化为(1-x2)[
•25+
•24•(-x)1+
•23•(-x)2+…+
•(-x)5],从而求得展开式含x2项的系数.
| C | 0 5 |
| C | 1 5 |
| C | 2 5 |
| C | 5 5 |
解答:
解:(1+x)(1-x)(2-x)5=(1-x2)[
•25+
•24•(-x)1+
•23•(-x)2+…+
•(-x)5],
故展开式含x2项的系数为
•23-
•25=48,
故选:B.
| C | 0 5 |
| C | 1 5 |
| C | 2 5 |
| C | 5 5 |
故展开式含x2项的系数为
| C | 2 5 |
| C | 0 5 |
故选:B.
点评:本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
对于四个命题p,q,r,m:已知p是q的充分条件,r是q的必要条件,p是r的充要条件,r是m的只充分条件,则m是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
若f(x)是R上的奇函数,则2f(0)的值等于( )
| A、0 | B、1 | C、2 | D、4 |
若复数
(m∈R)的实部与虚部的和为零,则m的值等于( )
| 2+mi |
| 1+i |
| A、0 | B、1 | C、2 | D、3 |
设△ABC中,内角A,B,C的对边分别为a,b,c,且c2=a2+b2-ab,那么△ABC的内角C等于( )
| A、30° | B、45° |
| C、60° | D、120° |
化简
的结果是( )
sin(
| ||||
| cos2x-sin2x |
| A、-1 | ||
| B、1 | ||
C、
| ||
D、-
|
已知
=-2,则tanx的值为( )
| 1-cosx+sinx |
| 1+cosx+sinx |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
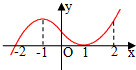 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: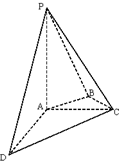 如图在四棱锥P-ABCD中,PA丄平面ABCD,AC丄AD,AB丄BC,∠BAC=45°,PA=AD=2,AC=1.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:
如图在四棱锥P-ABCD中,PA丄平面ABCD,AC丄AD,AB丄BC,∠BAC=45°,PA=AD=2,AC=1.建立适当的空间直角坐标系,利用空间向量方法解答以下问题: