题目内容
判断并证明函数f(x)=
+x的单调性.
| 2x-1 |
考点:函数单调性的判断与证明
专题:证明题
分析:利用函数单调性的定义可进行证明,要注意先进行判断,再利用作差法进行证明.
解答:
解:函数f(x)=
+x在[
,+∞)上是单调递增函数,证明如下:
由题意得:2x-1≥0,解得:x≥
;
∴函数f(x)的定义域为:[
,+∞),
设x1>x2,x1,x2∈[
,∞),
∴f(x1)-f(x2)=
+x1-(
+x2)
=(
-
)+(x1-x2)
∵x1>x2,∴x1-x2>0,2x1-1>2x2-1,
∴
>
∴f(x1)>f(x2)
∴结论得证.
| 2x-1 |
| 1 |
| 2 |
由题意得:2x-1≥0,解得:x≥
| 1 |
| 2 |
∴函数f(x)的定义域为:[
| 1 |
| 2 |
设x1>x2,x1,x2∈[
| 1 |
| 2 |
∴f(x1)-f(x2)=
| 2x1-1 |
| 2x2-1 |
=(
| 2x1-1 |
| 2x2-1 |
∵x1>x2,∴x1-x2>0,2x1-1>2x2-1,
∴
| 2x1-1 |
| 2x2-1 |
∴f(x1)>f(x2)
∴结论得证.
点评:本题考查了函数单调性的定义,证明过程要环环相扣,特别是重要的步骤要清晰明了.

练习册系列答案
相关题目
设△ABC中,内角A,B,C的对边分别为a,b,c,且c2=a2+b2-ab,那么△ABC的内角C等于( )
| A、30° | B、45° |
| C、60° | D、120° |
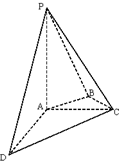 如图在四棱锥P-ABCD中,PA丄平面ABCD,AC丄AD,AB丄BC,∠BAC=45°,PA=AD=2,AC=1.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:
如图在四棱锥P-ABCD中,PA丄平面ABCD,AC丄AD,AB丄BC,∠BAC=45°,PA=AD=2,AC=1.建立适当的空间直角坐标系,利用空间向量方法解答以下问题: