题目内容
袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是
,从B中摸出一个红球的概率为p.
(Ⅰ)从A中有放回地摸球,每次摸出一个,共摸5次.求恰好有2次摸到红球但不连续的概率;
(Ⅱ)若A、B两个袋子中的球数之比为1:2,将A、B中的球装在一起后,从中摸出一个红球的概率是
,求p的值.
| 1 |
| 3 |
(Ⅰ)从A中有放回地摸球,每次摸出一个,共摸5次.求恰好有2次摸到红球但不连续的概率;
(Ⅱ)若A、B两个袋子中的球数之比为1:2,将A、B中的球装在一起后,从中摸出一个红球的概率是
| 2 |
| 5 |
考点:n次独立重复试验中恰好发生k次的概率,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)每次摸出一个红球的概率是
,出现红球的情况共有6种,故恰好有2次摸到红球但不连续的概率为 6×(
×
)×(
)3,计算求得结果.
(Ⅱ)根据A、B两个袋子中的球数之比为1:2,将A、B中的球装在一起后,从中摸出一个红球的概率是
,得到两个方程,即可求得概率.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
(Ⅱ)根据A、B两个袋子中的球数之比为1:2,将A、B中的球装在一起后,从中摸出一个红球的概率是
| 2 |
| 5 |
解答:
解:(Ⅰ)从A中有放回地摸球,每次摸出一个,共摸5次,每次摸出一个红球的概率是
,
出现红球的情况可能是 第一次、第三次;或第一次、第四次;或第一次、第五次;或第二次、第四次;或
第二次、第五次;或第三次、第五次,共有6种情况,
故恰好有2次摸到红球但不连续的概率为 6×(
×
)×(
)3=
.
(Ⅱ)设A中有x个球,B中有y个球,则
∵A、B两个袋子中的球数之比为1:2,将A、B中的球装在一起后,从中摸出一个红球的概率是
,
∴
=
,且
=
,∴p=
.
故选B.
| 1 |
| 3 |
出现红球的情况可能是 第一次、第三次;或第一次、第四次;或第一次、第五次;或第二次、第四次;或
第二次、第五次;或第三次、第五次,共有6种情况,
故恰好有2次摸到红球但不连续的概率为 6×(
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 16 |
| 81 |
(Ⅱ)设A中有x个球,B中有y个球,则
∵A、B两个袋子中的球数之比为1:2,将A、B中的球装在一起后,从中摸出一个红球的概率是
| 2 |
| 5 |
∴
| ||
| x+y |
| 2 |
| 5 |
| x |
| y |
| 1 |
| 2 |
| 13 |
| 30 |
故选B.
点评:本题考查概率的计算,考查学生的理解能力,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
化简
的结果是( )
sin(
| ||||
| cos2x-sin2x |
| A、-1 | ||
| B、1 | ||
C、
| ||
D、-
|
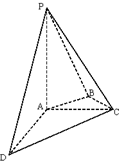 如图在四棱锥P-ABCD中,PA丄平面ABCD,AC丄AD,AB丄BC,∠BAC=45°,PA=AD=2,AC=1.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:
如图在四棱锥P-ABCD中,PA丄平面ABCD,AC丄AD,AB丄BC,∠BAC=45°,PA=AD=2,AC=1.建立适当的空间直角坐标系,利用空间向量方法解答以下问题: