题目内容
计算:
(1)
(
+
+
)dx
(2)若复数z1=a+2i(a∈R),z2=3-4i,且
为纯虚数,求|z1|.
(1)
| ∫ | 2 1 |
| 1 | ||
|
| 1 |
| x |
| 1 |
| x2 |
(2)若复数z1=a+2i(a∈R),z2=3-4i,且
| z1 |
| z2 |
考点:复数求模,微积分基本定理
专题:导数的综合应用,数系的扩充和复数
分析:(1)利用导数的运算法则和微积分基本定理即可得出;
(2)利用复数的运算法则和纯虚数的意义即可得出.
(2)利用复数的运算法则和纯虚数的意义即可得出.
解答:
解:(1)原式=(2
+lnx-
)
=2
-
+ln2.
(2)
=
=
=
+
i为纯虚数,
∴
,解得a=
,
∴Z1=
+2i,
∴|Z1|=
=
.
| x |
| 1 |
| x |
| | | 2 1 |
| 2 |
| 3 |
| 2 |
(2)
| Z1 |
| Z2 |
| a+2i |
| 3-4i |
| 3a-8+(6+4a)i |
| 25 |
| 3a-8 |
| 25 |
| 6+4a |
| 25 |
∴
|
| 8 |
| 3 |
∴Z1=
| 8 |
| 3 |
∴|Z1|=
(
|
| 10 |
| 3 |
点评:本题考查了导数的运算法则和微积分基本定理、复数的运算法则和纯虚数的意义,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
对于四个命题p,q,r,m:已知p是q的充分条件,r是q的必要条件,p是r的充要条件,r是m的只充分条件,则m是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
化简
的结果是( )
sin(
| ||||
| cos2x-sin2x |
| A、-1 | ||
| B、1 | ||
C、
| ||
D、-
|
已知
=-2,则tanx的值为( )
| 1-cosx+sinx |
| 1+cosx+sinx |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
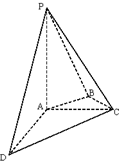 如图在四棱锥P-ABCD中,PA丄平面ABCD,AC丄AD,AB丄BC,∠BAC=45°,PA=AD=2,AC=1.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:
如图在四棱锥P-ABCD中,PA丄平面ABCD,AC丄AD,AB丄BC,∠BAC=45°,PA=AD=2,AC=1.建立适当的空间直角坐标系,利用空间向量方法解答以下问题: