题目内容
下列命题中正确的有 .(填上所有正确命题的序号)
①若f′(x0)=0,则函数y=f(x)在x=x0取得极值;
②直线5x-2y+1=0与函数f(x)=sin(2x+
)的图象不相切.
③若z∈C(C为复数集)且|z+2-2i|=1,则|z-2-2i|的最小值是3
④定积分
dx=4π.
①若f′(x0)=0,则函数y=f(x)在x=x0取得极值;
②直线5x-2y+1=0与函数f(x)=sin(2x+
| π |
| 3 |
③若z∈C(C为复数集)且|z+2-2i|=1,则|z-2-2i|的最小值是3
④定积分
| ∫ | 0 -4 |
| 16-x2 |
考点:命题的真假判断与应用
专题:阅读型,导数的综合应用,数系的扩充和复数
分析:①举反例,比如f(x)=x3,f′(0)=0,加以判断即可;
②求出导数f′(x),由切线的斜率等于f′(x0),根据三角函数的值域加以判断即可;
③|z+2-2i|=1表示圆,|z-2-2i|的几何意义两点的距离,通过连接两定点,由原定特性即可求出最小值;
④令y=
,则x2+y2=16(y≥0),点(x,y)的轨迹表示半圆,则该积分表示该圆面积的
.
②求出导数f′(x),由切线的斜率等于f′(x0),根据三角函数的值域加以判断即可;
③|z+2-2i|=1表示圆,|z-2-2i|的几何意义两点的距离,通过连接两定点,由原定特性即可求出最小值;
④令y=
| 16-x2 |
| 1 |
| 4 |
解答:
解:①比如f(x)=x3,f′(0)=0,但x=0不是极值点,是因为x=0处的导数同号,故①错;
②若直线与函数的图象相切,则f′(x0)=
,即2cos(2x0+
)=
,显然x0不存在,故②正确;
③|z+2-2i|=1的几何意义是以A(-2,2)为圆心,半径为1的圆,|z-2-2i|的几何意义是圆上一点到点B(2,2)的距离,连接AB并延长,显然最小值为AB-1=4-1=3,故③正确;
④令y=
,则x2+y2=16(y≥0),点(x,y)的轨迹表示半圆,定积分
dx
表示以原点为圆心,4为半径的圆面积的
,故定积分
dx=
×π×42=4π,故④正确.
故答案为:②③④
②若直线与函数的图象相切,则f′(x0)=
| 5 |
| 2 |
| π |
| 3 |
| 5 |
| 2 |
③|z+2-2i|=1的几何意义是以A(-2,2)为圆心,半径为1的圆,|z-2-2i|的几何意义是圆上一点到点B(2,2)的距离,连接AB并延长,显然最小值为AB-1=4-1=3,故③正确;
④令y=
| 16-x2 |
| ∫ | 0 -4 |
| 16-x2 |
表示以原点为圆心,4为半径的圆面积的
| 1 |
| 4 |
| ∫ | 0 -4 |
| 16-x2 |
| 1 |
| 4 |
故答案为:②③④
点评:本题以命题的真假为载体考查函数的极值概念,导数的应用于求切线方程,以及复数的几何意义,定积分的几何意义及求法,是一道基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
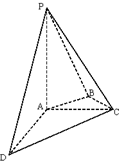 如图在四棱锥P-ABCD中,PA丄平面ABCD,AC丄AD,AB丄BC,∠BAC=45°,PA=AD=2,AC=1.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:
如图在四棱锥P-ABCD中,PA丄平面ABCD,AC丄AD,AB丄BC,∠BAC=45°,PA=AD=2,AC=1.建立适当的空间直角坐标系,利用空间向量方法解答以下问题: