题目内容
15．在半径为1的圆O内任取一点M，过M且垂直OM与直线l与圆O交于圆A，B两点，则AB长度大于$\sqrt{3}$的概率为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{1}{2}$ |
分析 由题意，|OM|≤$\sqrt{1-\frac{3}{4}}$=$\frac{1}{2}$，以面积为测度，可得AB长度大于$\sqrt{3}$的概率．
解答 解：由题意，|OM|≤$\sqrt{1-\frac{3}{4}}$=$\frac{1}{2}$，
以面积为测度，可得AB长度大于$\sqrt{3}$的概率为$\frac{π•\frac{1}{4}}{π•{1}^{2}}$=$\frac{1}{4}$，
故选A．
点评 本题主要考查几何概型中的面积类型，解决的关键是找到问题的分界点，分清是长度，面积，还是体积类型，再应用概率公式求解．
练习册系列答案
相关题目
5．已知向量$\overrightarrow{OA}=（{3，1}），\overrightarrow{OB}=（{-1，3}）$，$\overrightarrow{OC}=m\overrightarrow{OA}-n\overrightarrow{OB}（{m＞0，n＞0}）$，若m+n=1，则$|{\overrightarrow{OC}}$|的最小值为（ ）
| A． | $\frac{{\sqrt{5}}}{2}$ | B． | $\frac{{\sqrt{10}}}{2}$ | C． | $\sqrt{5}$ | D． | $\sqrt{10}$ |
6．设函数f（x）=$\left\{\begin{array}{l}{lo{g}_{0.2}x，x∈（1，+∞）}\\{2-2x，x∈（-∞，1]}\end{array}\right.$，若a=f（20.3），b=f（log0.32），c=f（log32），则a、b、c的大小关系是（ ）
| A． | b＞c＞a | B． | b＞a＞c | C． | a＞c＞b | D． | a＞b＞c |
3．
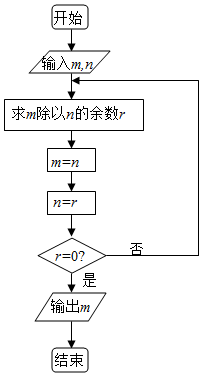阅读如图所示的程序框图，运行相应的程序，若输入m=168，n=72，则输出m的值为（ ）
阅读如图所示的程序框图，运行相应的程序，若输入m=168，n=72，则输出m的值为（ ）| A． | 72 | B． | 24 | C． | 12 | D． | 6 |
10．
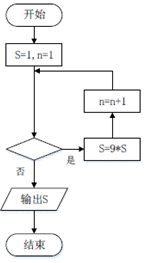我国古代算书《孙子算经》上有个有趣的问题“出门望九堤”：今有出门重九堤，堤有九木，木有九枝，枝有九巢，巢有九禽，禽有九雏，雏有九毛，毛有九色，问各几何？现在我们用右图所示的程序框图来解决这个问题，如果要使输出的结果为禽的数目，则在该框图中的判断框中应该填入的条件是（ ）
我国古代算书《孙子算经》上有个有趣的问题“出门望九堤”：今有出门重九堤，堤有九木，木有九枝，枝有九巢，巢有九禽，禽有九雏，雏有九毛，毛有九色，问各几何？现在我们用右图所示的程序框图来解决这个问题，如果要使输出的结果为禽的数目，则在该框图中的判断框中应该填入的条件是（ ）| A． | S＞10000？ | B． | S＜10000？ | C． | n≥5 | D． | n≤6 |
7．已知2a+2b=2c，则a+b-2c的最大值等于（ ）
| A． | -2 | B． | -1 | C． | $\frac{1}{4}$ | D． | -$\frac{1}{4}$ |
8．已知3cos2θ=tanθ+3，且θ≠kπ（k∈Z），则sin[2（π-θ）]等于（ ）
| A． | -$\frac{1}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | -$\frac{2}{3}$ |