题目内容
14.设E,F分别是正方形ABCD的边AB,BC上的点,且$AE=\frac{1}{2}AB$,$BF=\frac{2}{3}BC$,如果$\overrightarrow{EF}=m\overrightarrow{AB}+n\overrightarrow{AC}$(m,n为实数),那么m+n的值为( )| A. | $-\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
分析 如图所示,$\overrightarrow{EF}=\overrightarrow{EA}+\overrightarrow{AC}+\overrightarrow{CF}$=$-\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AC}-\frac{1}{3}\overrightarrow{BC}$=-$\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AC}-\frac{1}{3}(\overrightarrow{BA}+\overrightarrow{AC})=-\frac{1}{6}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$.即可求得m,n即可.
解答 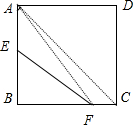 解:如图所示,$\overrightarrow{EF}=\overrightarrow{EA}+\overrightarrow{AC}+\overrightarrow{CF}$=$-\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AC}-\frac{1}{3}\overrightarrow{BC}$
解:如图所示,$\overrightarrow{EF}=\overrightarrow{EA}+\overrightarrow{AC}+\overrightarrow{CF}$=$-\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AC}-\frac{1}{3}\overrightarrow{BC}$
=-$\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AC}-\frac{1}{3}(\overrightarrow{BA}+\overrightarrow{AC})=-\frac{1}{6}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$.
∴m=-$\frac{1}{6}$,n=$\frac{2}{3}$,∴$m+n=\frac{1}{2}$,
故选:C
点评 本题考查了向量的线性运算,合理利用向量的平行四边形法则,三角形法则,是解题关键,属于基础题.

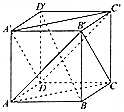
| A. | 平面ACB′∥平面A′C′D | B. | B′C⊥BD′ | ||
| C. | B′C⊥DC′ | D. | BD′⊥平面A′C′D |
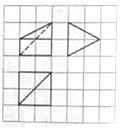 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某四棱锥的三视图,则该四棱锥各个侧面中,最大的侧面面积为( )
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某四棱锥的三视图,则该四棱锥各个侧面中,最大的侧面面积为( )| A. | 2 | B. | $\sqrt{5}$ | C. | 3 | D. | 4 |
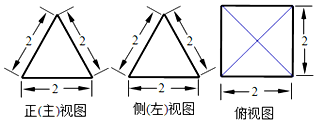
| A. | 16 | B. | 12 | C. | $\frac{4\sqrt{3}}{3}$+4 | D. | 4$\sqrt{3}$+4 |
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |