题目内容

6．如图是一个空间几何体的三视图，则该几何体的表面积为（　　）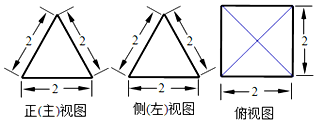 
A．16B．12C．$\frac{4\sqrt{3}}{3}$+4D．4$\sqrt{3}$+4

分析 由三视图可得，直观图是正四棱锥，底面是正方形，斜高为2，即可求出该几何体的表面积．

解答 解：由三视图可得，直观图是正四棱锥，底面是正方形，斜高为2，该几何体的表面积为$2×2+4×2×2×\frac{1}{2}$=12，
故选B．

点评 本题考查由三视图求面积，考查学生的计算能力，确定直观图的形状是关键．

练习册系列答案
相关题目
16．已知集合A={x|x2+2x-3≤0}，B={x|0≤log4（x+2）≤1}，则A∩B=（　　）
A．[-3，2]B．[-1，1]C．[-1，2]D．[1，2]
17．已知集合A={x|y=lgx}，B={x|x2-2x-3＜0}，则A∩B=（0，3）．
14．设E，F分别是正方形ABCD的边AB，BC上的点，且$AE=\frac{1}{2}AB$，$BF=\frac{2}{3}BC$，如果$\overrightarrow{EF}=m\overrightarrow{AB}+n\overrightarrow{AC}$（m，n为实数），那么m+n的值为（　　）
A．$-\frac{1}{2}$B．0C．$\frac{1}{2}$D．1
1．如果执行如图的程序框图，且输入n=4，m=3，则输出的p=（　　）
A．6B．24C．120D．720
11．设函数f（x）=ln（x+1）+a（x2-x），其中a∈R
（1）讨论函数f（x）极值点的个数，并说明理由；
（2）若任意x∈（0，+∞），f（x）＞0成立，求a的取值范围．
18．已知函数f（x）=x-aln x．
（1）求函数f（x）的单调区间；
（2）当x=2时，函数f（x）取得极小值，求a的值；
（3）若函数f（x）有两个零点，求a的取值范围．
15．已知函数f（x）=|x-1|+|x-5|，g（x）=$\sqrt{1+{x}^{2}}$．
（1）求f（x）的最小值；
（2）记f（x）的最小值为m，已知实数a，b满足a2+b2=6，求证：g（a）+g（b）≤m．
16．中国古代数学著作《算法统宗》中记载了这样一个问题：“三百七十八里关，出行健步不为难，次日脚疼减一半，六朝才得到其关，要见次日行里数，请公仔细算相还．”其大意为：“有一人走了378里路，第一天健步行走，从第二天起因脚疼每天走的路程为前一天的一半，走了6天后到达目的地．”问此人第二天天走了（　　）里？
A．76B．96C．146D．188

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网