题目内容
已知f(x)为偶函数,当x≥0时,f(x)=
,则不等式f(x)≤
的解集为( )
|
| 1 |
| 2 |
A、[-
| ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[
|
考点:其他不等式的解法,分段函数的应用
专题:不等式的解法及应用
分析:当x∈[0,
]时,根据余弦函数的图象求出f(x)≤
的解集,当x>
时,求出f(x)≤
的解集,可得当x≥0时,不等式f(x)≤
的解集.再根据偶函数的性质,
求得当x<0时,f(x)≤
的解集,综合可得结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
求得当x<0时,f(x)≤
| 1 |
| 2 |
解答:
解:当x≥0时,若x∈[0,
],则πx∈[0,
]由不等式f(x)≤
,可得cosπx≤
,
可得
≤πx≤
,∴
≤x≤
,它的解集为[
,
].
若x>
,不等式f(x)≤
,即2x-1≤
,它的解集为{x|
<x≤
}.
综上可得,当x≥0时,不等式的解集为{x|
<x≤
},
再根据f(x)为偶函数,可得在R上,不等式的解集为{x|
<x≤
,或-
≤x<-
},
故选:B.
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
可得
| π |
| 3 |
| π |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
若x>
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
综上可得,当x≥0时,不等式的解集为{x|
| 1 |
| 3 |
| 3 |
| 4 |
再根据f(x)为偶函数,可得在R上,不等式的解集为{x|
| 1 |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 3 |
故选:B.
点评:本题主要考查分段函数的应用,函数的奇偶性的性质,三角不等式的解法,余弦函数的图象,属于基础题.

练习册系列答案
相关题目
已知集合A={x|x>4或x<-1},B={x|ax-1>0},若A∪B=A,则实数a的取值范围是( )
A、(0,
| ||
B、(-1,0)∪(0,
| ||
C、(-1,
| ||
D、[-1,
|
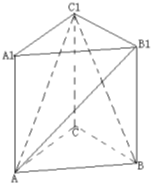 (文)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=2.
(文)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=2.