题目内容

已知函数f（x）=
x
x2+1
，求证：函数f（x）是奇函数．
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：首先判断函数的定义域为R，然后利用奇偶函数的定义，证明f（-x）=-f（x）．
解答： 解：由已知，f（x）的定义域为R，关于原点对称，
并且f（-x）=
-x
(-x)2+1
=-
x
x2+1
=-f（x），
∴函数f（x）是奇函数．
点评：本题考查了函数奇偶性的证明；在明确定义域的前提下，再利用定义证明．
练习册系列答案
相关题目
求函数y=
2x
3x-4
的值域．
已知t是实数，求函数f（x）=x2+|x-t|-1的最小值．
（1）如图1是将正方体沿着共点的三条棱的中点A、B、C截 去一个三棱锥后剩下的几何体．画出该几何体的三视图．
（2）已知某个几何体的三视图如图2，根据图中标出的数据，可得这个几何体的体积是多少？
已知f（x）为偶函数，当x≥0时，f（x）=
cosπx，x∈[0，
1
2
]
2x-1，x∈(
1
2
，+∞)
，则不等式f（x）≤
1
2
的解集为（　　）
A、[-
3
4
，-
2
3
]∪[
2
3
，
3
4
]
B、[-
3
4
，-
1
3
]∪[
1
3
，
3
4
]
C、[-
7
4
，-
1
3
]∪[
1
3
，
7
4
]
D、[
1
4
，
2
3
]∪[
4
3
，
7
4
]
给出下列五个命题：
①函数y=tanx的图象关于点（kπ+
π
2
，0）（k∈Z）对称；
②函数f（x）=tanx是最小正周期为π的周期函数；
③函数y=cos2x+sinx的最小值为-1；
④设θ为第二象限的角，则tan
θ
2
＞cos
θ
2
，且sin
θ
2
＞cos
θ
2
；
⑤若θ第三象限角，则点P（sin（cosθ），cos（cosθ））在第二象限．
其中正确的命题序号是
 
．．
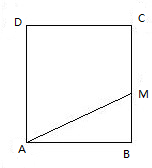已知正方形ABCD的边长为2，有一动点M从点B出发沿正方形的边运动，路线是B→C→D→A，设点M经过的路程为x，△ABM的面积为S，求函数S=f（x）的解析式及其定义域．
数列{an}满足条件a1=1，an=an-1+（
1
3
）n-1（n=2，3，…）．
（1）求{an}；
（2）求a1+a2+a3+…+an．
已知
1
a
，
1
b
，
1
c
是等差数列，求证：
b+c-a
a
，
a+c-b
b
，
a+b-c
c
也是等差数列．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网