题目内容
已知集合A={x|x>4或x<-1},B={x|ax-1>0},若A∪B=A,则实数a的取值范围是( )
A、(0,
| ||
B、(-1,0)∪(0,
| ||
C、(-1,
| ||
D、[-1,
|
考点:子集与交集、并集运算的转换
专题:集合
分析:根据A∪B=A得B⊆A,所以要求集合B,所以讨论a的取值:a=0,a>0,a<0,根据B⊆A,分别求出这三种情况下的a的取值,求并集即可.
解答:
解:A∪B=A,∴B⊆A;
若a=0,B=∅满足条件;
若a>0,B={x|x>
},则
≥4,∴0<a≤
;
若a<0,B={x|x<
},则
≤-1,∴-1≤a<0;
综上得a的取值范围是:[-1,
].
故选D.
若a=0,B=∅满足条件;
若a>0,B={x|x>
| 1 |
| a |
| 1 |
| a |
| 1 |
| 4 |
若a<0,B={x|x<
| 1 |
| a |
| 1 |
| a |
综上得a的取值范围是:[-1,
| 1 |
| 4 |
故选D.
点评:考查并集、子集的概念,不要漏了a=0的情况.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
已知f(x)为偶函数,当x≥0时,f(x)=
,则不等式f(x)≤
的解集为( )
|
| 1 |
| 2 |
A、[-
| ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[
|
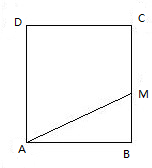 已知正方形ABCD的边长为2,有一动点M从点B出发沿正方形的边运动,路线是B→C→D→A,设点M经过的路程为x,△ABM的面积为S,求函数S=f(x)的解析式及其定义域.
已知正方形ABCD的边长为2,有一动点M从点B出发沿正方形的边运动,路线是B→C→D→A,设点M经过的路程为x,△ABM的面积为S,求函数S=f(x)的解析式及其定义域.