题目内容
已知甲、乙两个盒子,甲盒中有2个黑球和2个红球,乙盒中有2个黑球和3个红球,从甲、乙两盒中各取一球交换.
(Ⅰ)求交换后甲盒中有2个黑球的概率;
(Ⅱ)设交换后甲盒中黑球的个数为ξ,求ξ的分布列及数学期望.
(Ⅰ)求交换后甲盒中有2个黑球的概率;
(Ⅱ)设交换后甲盒中黑球的个数为ξ,求ξ的分布列及数学期望.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(Ⅰ)①互换的黑球,②互换的是红球,分别求出概率,然后求解甲盒中有2个黑球的概率.
(2)设甲盒中黑球的个数为ξ,求出ξ的分布列,然后求出期望.
(2)设甲盒中黑球的个数为ξ,求出ξ的分布列,然后求出期望.
解答:
16 解:(Ⅰ)①互换的黑球,此时甲盒子恰好有2黑球的事件记为A1,则:P(A1)=
=
,
②互换的是红球,此时甲甲盒子恰好有2黑球记为A2,则:P(A2)=
=
故甲盒中有2个黑球的概率P=P(A1)+P(A2)=
+
=
(2)设甲盒中黑球的个数为ξ,则:P(ξ=1)=
=
;
P(ξ=2)=
;
P(ξ=3)=
=
,
因而ξ的分布列为:
∴Eξ=
×1+
×2+
×3=
.
| ||||
|
| 1 |
| 5 |
②互换的是红球,此时甲甲盒子恰好有2黑球记为A2,则:P(A2)=
| ||||
|
| 3 |
| 10 |
故甲盒中有2个黑球的概率P=P(A1)+P(A2)=
| 1 |
| 5 |
| 3 |
| 10 |
| 1 |
| 2 |
(2)设甲盒中黑球的个数为ξ,则:P(ξ=1)=
| ||||
|
| 3 |
| 10 |
P(ξ=2)=
| 1 |
| 2 |
P(ξ=3)=
| ||||
|
| 1 |
| 5 |
因而ξ的分布列为:
| ξ | 1 | 2 | 3 | ||||||
| p |
|
|
|
| 3 |
| 10 |
| 1 |
| 2 |
| 1 |
| 5 |
| 19 |
| 10 |
点评:本题考查离散型随机变量的分布列的求法,期望以及概率的求法,考查计算能力.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
等差数列{an}中,a1=1,a2=3,数列{
}的前n项和为
,则n的值为( )
| 1 |
| anan+1 |
| 15 |
| 31 |
| A、15 | B、16 | C、17 | D、18 |
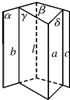 求证:如果一条直线和两个相交的平面都平行,那么这条直线和它们的交线平行,已知:如图,α∩β=l,a∥α,a∥β,求证:a∥l.
求证:如果一条直线和两个相交的平面都平行,那么这条直线和它们的交线平行,已知:如图,α∩β=l,a∥α,a∥β,求证:a∥l.