题目内容
函数y=sinx与y=cosx,它们的周期是 ,定义域是 .
考点:三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:由正弦函数,余弦函数的图象和性质即可解得.
解答:
解:由正弦函数,余弦函数的图象和性质可得:
函数y=sinx与y=cosx,它们的周期是:2π,定义域是:R.
故答案为:2π,R.
函数y=sinx与y=cosx,它们的周期是:2π,定义域是:R.
故答案为:2π,R.
点评:本题主要考查了正弦函数,余弦函数的图象和性质,属于基础题.

练习册系列答案
相关题目
在某项测量中,测量结果ξ服从正态分布N(0,σ2)(σ>0),若P(ξ<-1)=0.1,则ξ在区间(0,1)内取值的概率为( )
| A、0.4 | B、0.5 |
| C、0.8 | D、0.9 |
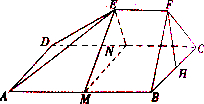 如图,多面体EF-ABCD中,已知ABCD是边长为4的正方形,EF∥AB,平面FBC⊥平面ABCD,EF=2.
如图,多面体EF-ABCD中,已知ABCD是边长为4的正方形,EF∥AB,平面FBC⊥平面ABCD,EF=2.