题目内容
等差数列{an}中,a1=1,a2=3,数列{
}的前n项和为
,则n的值为( )
| 1 |
| anan+1 |
| 15 |
| 31 |
| A、15 | B、16 | C、17 | D、18 |
考点:数列的求和
专题:等差数列与等比数列
分析:求出数列的通项公式,利用裂项法求法数列的和,求出n即可.
解答:
解:等差数列{an}中,a1=1,a2=3,d=2,an=2n-1,
数列
=
=
(
-
).
数列{
}的前n项和为
,
∴
(
-
+
-
+…+
-
)=
=
,
解得n=15.
故选:A.
数列
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
数列{
| 1 |
| anan+1 |
| 15 |
| 31 |
∴
| 1 |
| 2 |
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 15 |
| 31 |
| n |
| 2n+1 |
| 15 |
| 31 |
解得n=15.
故选:A.
点评:本题考查等差数列通项公式的求法,数列求和的方法,考查计算能力.

练习册系列答案
相关题目
 如图所示,一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰为2的等腰三角形,那么原平面图形的面积是( )
如图所示,一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰为2的等腰三角形,那么原平面图形的面积是( )| A、2 | ||
B、2
| ||
C、4
| ||
D、8
|
已知函数f(x)=xα,α∈{-1,
,1,2,3},若f(x)是区间(-∞,+∞)上的增函数,则α的所有可能取值为( )
| 1 |
| 2 |
| A、{1,3} | ||
B、{
| ||
| C、{1,2,3} | ||
D、{-1,
|
函数f(x)=[x]的函数值表示不超过x的最大整数,例如,[-3.5]=-4,[2.1]=2.当x∈(-2.5,3]时,函数f(x)的值域为( )
| A、{-2,-1,0,1,2} |
| B、{-3,-2,-1,0,1,2} |
| C、{-2,-1,0,1,2,3} |
| D、{-3,-2,-1,0,1,2,3} |
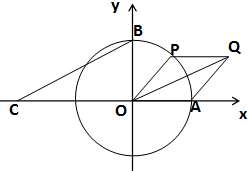 如图所示,A、B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),点C坐标为(-2,0),平行四边形OAQP的面积为S.
如图所示,A、B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),点C坐标为(-2,0),平行四边形OAQP的面积为S.