题目内容
平面上,到点F(1,0)的距离与它到直线l:x=-1的距离相等的动点P的轨迹记作曲线C.
(1)求曲线C的方程;
(2)若倾斜角为
的直线m过点F,且与曲线C相交于A,B两点,求线段AB的长.
(1)求曲线C的方程;
(2)若倾斜角为
| π |
| 4 |
考点:轨迹方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)根据抛物线的定义,可求动点P的轨迹C的方程;
(2)直线m的方程代入y2=4x,可得y2=4y+4,即可求线段AB的长.
(2)直线m的方程代入y2=4x,可得y2=4y+4,即可求线段AB的长.
解答:
解:(1)依题意,动点P的轨迹C是以F(1,0)为焦点,l:x=-1为准线的抛物线,
设轨迹C的方程为y2=2px(p>0),则p=2所以动点P的轨迹C的方程为y2=4x;
(2)直线m的方程为y=x-1,即x=y+1,
代入y2=4x,可得y2=4y+4,
所以|AB|=
•
=2
.
设轨迹C的方程为y2=2px(p>0),则p=2所以动点P的轨迹C的方程为y2=4x;
(2)直线m的方程为y=x-1,即x=y+1,
代入y2=4x,可得y2=4y+4,
所以|AB|=
| 1+1 |
| 4+16 |
| 10 |
点评:定义法是求圆锥曲线方程的重要方法,解决直线与圆锥曲线位置关系问题,通常联立方程.

练习册系列答案
相关题目
 如图所示,一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰为2的等腰三角形,那么原平面图形的面积是( )
如图所示,一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰为2的等腰三角形,那么原平面图形的面积是( )| A、2 | ||
B、2
| ||
C、4
| ||
D、8
|
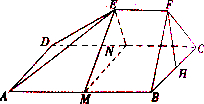 如图,多面体EF-ABCD中,已知ABCD是边长为4的正方形,EF∥AB,平面FBC⊥平面ABCD,EF=2.
如图,多面体EF-ABCD中,已知ABCD是边长为4的正方形,EF∥AB,平面FBC⊥平面ABCD,EF=2.