题目内容
已知函数f(x)=sin(ωx+φ) 图象的相邻两条对称轴之间的距离等于
,cos(φ+
)=0,其中ω>0,|φ|<
.
(1)求函数f(x)的解析式;
(2)求最小正实数m,使得函数f(x)的图象向左平移m个单位后所对应的函数是偶函数.
| π |
| 3 |
| π |
| 4 |
| π |
| 2 |
(1)求函数f(x)的解析式;
(2)求最小正实数m,使得函数f(x)的图象向左平移m个单位后所对应的函数是偶函数.
考点:正弦函数的图象,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)根据函数的性质求出ω 和φ,即可求函数f(x)的解析式;
(2)利用三角函数的图象关系,结合三角函数的奇偶性即可得到结论.
(2)利用三角函数的图象关系,结合三角函数的奇偶性即可得到结论.
解答:
解:(1)∵cos(φ+
)=0,
∴φ+
=kπ+
(k∈Z),
∴φ=kπ+
(k∈Z),
又∵|φ|<
,∴φ=
.
∵相邻两条对称轴间的距离为
,
∴
=
,∴T=
,∴ω=
=3,
∴f(x)=sin(3x+
).
(2)f(x)的图象向左平移m个单位后得g(x)=sin[3(x+m)+
]=sin(3x+3m+
).
若g(x)是偶函数,当且仅当3m+
=kπ+
(k∈Z),
即m=
+
(k∈Z),
从而,最小正实数m=
.
| π |
| 4 |
∴φ+
| π |
| 4 |
| π |
| 2 |
∴φ=kπ+
| π |
| 4 |
又∵|φ|<
| π |
| 2 |
| π |
| 4 |
∵相邻两条对称轴间的距离为
| π |
| 3 |
∴
| T |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| T |
∴f(x)=sin(3x+
| π |
| 4 |
(2)f(x)的图象向左平移m个单位后得g(x)=sin[3(x+m)+
| π |
| 4 |
| π |
| 4 |
若g(x)是偶函数,当且仅当3m+
| π |
| 4 |
| π |
| 2 |
即m=
| kπ |
| 3 |
| π |
| 12 |
从而,最小正实数m=
| π |
| 12 |
点评:本题主要考查函数解析式的求解以及函数图象的平移变换,求出函数的解析式是解决本题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知函数f(x)=xα,α∈{-1,
,1,2,3},若f(x)是区间(-∞,+∞)上的增函数,则α的所有可能取值为( )
| 1 |
| 2 |
| A、{1,3} | ||
B、{
| ||
| C、{1,2,3} | ||
D、{-1,
|
为了得到函数f(x)=2sin(2x-
)的图象,只要将y=2sinx的图象上所有的点( )
| π |
| 3 |
A、向右平移
| ||||
B、向右平移
| ||||
C、向右平移
| ||||
D、向右平移
|
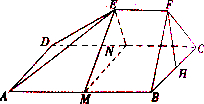 如图,多面体EF-ABCD中,已知ABCD是边长为4的正方形,EF∥AB,平面FBC⊥平面ABCD,EF=2.
如图,多面体EF-ABCD中,已知ABCD是边长为4的正方形,EF∥AB,平面FBC⊥平面ABCD,EF=2.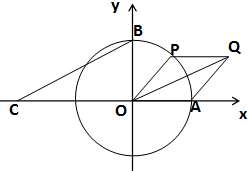 如图所示,A、B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),点C坐标为(-2,0),平行四边形OAQP的面积为S.
如图所示,A、B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),点C坐标为(-2,0),平行四边形OAQP的面积为S.