Question

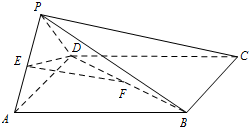如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，E，F分别为PA，BD中点，PA=PD=AD=2．
（Ⅰ）求证：EF∥平面PBC；
（Ⅱ）求二面角E-DF-A的余弦值；
（Ⅲ）在棱PC上是否存在一点G，使GF⊥平面EDF？若存在，指出点G的位置；若不存在，说明理由．

Answer 1

考点：直线与平面平行的判定,与二面角有关的立体几何综合题

专题：空间位置关系与距离

分析：（Ⅰ）作AB的中点H，连接EH，FH，先利用面面平行的判定定理证明出平面EFH∥平面PBC，进而根据面面平行的性质证明出EF∥平面PBC．
（Ⅱ）做EI垂直AD于I，作IJ⊥DB=J，连接EJ，做AD中点O，连接OP，先证明出∠EJI为二面角E-DF-A的平面角，进而求得JI和EJ，最后在直角三角形中求得cos∠EJI．
（Ⅲ）先假设存在点G，建立空间直角坐标系，求得平面EFD的一个法向量，仅而表示出

PC

和

CG

，根据向量共线的性质建立等式对λ求解．

解答： （Ⅰ）作AB的中点H，连接EH，FH，
∵在△PAB中，E，H为中点，
∴EH∥PB，
∵EH?平面PBC，PB?平面PBC，
∴EH∥平面PBC，
同理可证明FH∥平面PBC，
∵EH?平面EFH，FH?平面EFH，EH∩FH=H，
∴平面EFH∥平面PBC，
∵EF?平面EFH，
∴EF∥平面PBC．
（Ⅱ）做EI垂直AD于I，作IJ⊥DB=J，连接EJ，做AD中点O，连接OP，
∵PA=PD，
∴OP⊥AB，
∵EI⊥AB，
∴EI∥OP，
∵E为中点，
∴EI=

1

2

OP=

3

2

，AE=

1

4

AB=

1

2

，
∵侧面PAD⊥底面ABCD，
∴EI⊥底面ABCD，
∵IJ⊥DB，
∴EJ⊥DB，
∴∠EJI为二面角E-DF-A的平面角，
∵∠ADB=∠JIB，∠DJI=∠DAB=90°，
∴△DJI∽△ADB，
∴

DI

DB

=

JI

AB

，

3 2

2 2

=

JI

2

，
∴JI=

3

2 2

∴EJ=

JI2+EI2

=

9 8 + 3 4

=

15

2 2

，
∴cos∠EJI=

JI

EJ

=

3

2 2 15 2 2

=

15

5

．
即二面角E-DF-A的余弦值为

15

5

．
（Ⅲ）不存在．
假设存在，连接AC，则F在AC上，EF为平面EDF和平面PAC的交线，
以O为原点，OA，OF，OP分别为xyz轴建立空间直角坐标系．则A（1，0，0），
B（1，2，0），C（1，2，0），D（1，0，0），P（O，O，

3

），E（

1

2

，0，

3

2

），F（0，1，0），
设G（x₁，y₁，z₁），则

FG

=（x₁，y₁，z₁），
设平面EFD的一个法向量是n=（x₀，y₀，z₀），
∵

n• DF =0 n• DE =0

，∴

x0+y0=1 3 2 x0+ 3 2 y0=0

，
即

y0=x0 z0=- 3 x0

，令x₀=1，则n=（1，-1，-

3

），
∵因为GF⊥面EDF，
∴

FG

=λn，
∴x₁=λ，y₁-1=-λ，z₁=-

3

λ，
∵

GC

，

PC

共线，

PC

=（-1，2，-

3

），

CG

=（x₁+1，y₁-2，z₁），
∴

x1+1

-1

=

y1-2

2

=

z1

- 3

，
∴

1+λ

-1

=

-λ-1

2

=

- 3 λ

- 3

，无解，
故在棱PC上不存在一点G，故在棱PC上不存在一点G，使GF⊥平面EDF．

点评：本题主要考查了线面平行的判定定理的应用，二面角的计算，法向量的运用．考查了学生分析和推理的能力．