题目内容
已知数列{an}满足a1=
,公差d=-
,前a项和Sa=-5,求a的值及通项公式an.
| 5 |
| 6 |
| 1 |
| 6 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:根据等差数列的前n项和公式建立方程关系即可得到结论.
解答:
解:∵a1=
,公差d=-
,前a项和Sa=-5,
∴Sa=
a+
×(-
)=-5,
即a2-11a-60=0,
即(a+4)(a-15)=0,解得a=15或a=-4(舍去),
则an=
+(n-1)(-
)=-
n+1.
| 5 |
| 6 |
| 1 |
| 6 |
∴Sa=
| 5 |
| 6 |
| a(a-1) |
| 2 |
| 1 |
| 6 |
即a2-11a-60=0,
即(a+4)(a-15)=0,解得a=15或a=-4(舍去),
则an=
| 5 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
点评:本题主要考查等差数列的通项公式和前n项和公式的计算,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=xsinx+cosx的导函数原点处的部分图象大致为( )
A、 |
B、 |
C、 |
D、 |
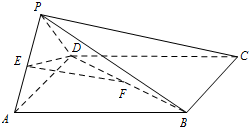 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2. 某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.