题目内容
已知函数f(x)=lnx-kx+1.
(1)若k=1,求函数f(x)的单调区间;
(2)若f(x)≤0恒成立,试确定实数k的取值范围.
(1)若k=1,求函数f(x)的单调区间;
(2)若f(x)≤0恒成立,试确定实数k的取值范围.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的概念及应用
分析:(1)把k=1代入求出导函数,得到单调区间,(2)先求出导函数,再通过讨论a的范围,求出函数的最值,解不等式求出即可.
解答:
解:f′(x)=
-k,x>0,
(1)k=1时,f′(x)=
-1,
令f′(x)>0,解得:0<x<1,
令f′(x)<0,解得:x>1,
∴f(x)在(0,1)递增,在(1,+∞)递减;
(2)k≤0时,f′(x)>0,f(x)递增,不合题意,
k>0时,令f′(x)>0,解得:0<x<
,
令f′(x)<0,解得:x>
,
∴f(x)在(0,
)递增,在(
,+∞)递减,
∴f(x)max=f(
)=-lnk,
若f(x)≤0恒成立,
∴-lnk≤0,
解得:k≥1,
∴k的范围是:(1,+∞).
| 1 |
| x |
(1)k=1时,f′(x)=
| 1 |
| x |
令f′(x)>0,解得:0<x<1,
令f′(x)<0,解得:x>1,
∴f(x)在(0,1)递增,在(1,+∞)递减;
(2)k≤0时,f′(x)>0,f(x)递增,不合题意,
k>0时,令f′(x)>0,解得:0<x<
| 1 |
| k |
令f′(x)<0,解得:x>
| 1 |
| k |
∴f(x)在(0,
| 1 |
| k |
| 1 |
| k |
∴f(x)max=f(
| 1 |
| k |
若f(x)≤0恒成立,
∴-lnk≤0,
解得:k≥1,
∴k的范围是:(1,+∞).
点评:本题考察了函数的单调性,导数的应用,渗透了分类讨论思想,是一道基础题.

练习册系列答案
相关题目
已知直线AB与抛物线y2=2x交于A,B两点,M是AB的中点,C是抛物线上的点,且使得
•
取最小值,抛物线在点C处的切线为l,则( )
| CA |
| CB |
| A、CM⊥AB | ||
| B、CM⊥l | ||
| C、CA⊥CB | ||
D、CM=
|
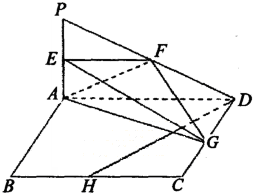 如图,四边形ABCD为正方形,PA⊥平面ABCD,且AD=2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.
如图,四边形ABCD为正方形,PA⊥平面ABCD,且AD=2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.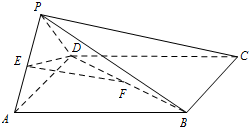 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2. 某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.