题目内容
已知a>b>0,且m=a+
.
(Ⅰ)试利用基本不等式求m的最小值t;
(Ⅱ)若实数x,y,z满足x+y+z=3且x2+4y2+z2=t,求证:|x+2y+z|≤3.
| 1 |
| (a-b)b |
(Ⅰ)试利用基本不等式求m的最小值t;
(Ⅱ)若实数x,y,z满足x+y+z=3且x2+4y2+z2=t,求证:|x+2y+z|≤3.
考点:二维形式的柯西不等式,基本不等式
专题:不等式的解法及应用
分析:(Ⅰ)由条件根据m=a+
=(a-b)+b+
,利用基本不等式求得m的最小值.
(Ⅱ)由条件利用柯西不等式求得当且仅当x=z=
,y=
时,9≥(x+2y+z)2 成立,从而证得结论.
| 1 |
| (a-b)b |
| 1 |
| (a-b)b |
(Ⅱ)由条件利用柯西不等式求得当且仅当x=z=
| 6 |
| 5 |
| 3 |
| 5 |
解答:
解:(Ⅰ)∵a>b>0,∴a-b>0,
m=a+
=(a-b)+b+
≥3
=3.
(当且仅当a-b=b=
,即b=1,a=2时取“=”号),
∴m的最小值t=3.
(Ⅱ)∵x+y+z=3,且x2+4y2+z2=t,由柯西不等式得:[且x2+(2y)2+z2]•(1+1+1)≥(x+2y+z)2,
(当且仅当
=
=
,即 x=z=
,y=
,时取“=”号)
整理得:9≥(x+2y+z)2,∴:|x+2y+z|≤3.
m=a+
| 1 |
| (a-b)b |
| 1 |
| (a-b)b |
| 3 | (a-b)b
| ||
(当且仅当a-b=b=
| 1 |
| (a-b)b |
∴m的最小值t=3.
(Ⅱ)∵x+y+z=3,且x2+4y2+z2=t,由柯西不等式得:[且x2+(2y)2+z2]•(1+1+1)≥(x+2y+z)2,
(当且仅当
| x |
| 1 |
| 2y |
| 1 |
| z |
| 1 |
| 6 |
| 5 |
| 3 |
| 5 |
整理得:9≥(x+2y+z)2,∴:|x+2y+z|≤3.
点评:本题主要考查基本不等式、柯西不等式等基础知识,考查推理论证能力,考查化归与转化思想,属于中档题.

练习册系列答案
相关题目
下列函数可用二分法求其在区间(0,1)内零点的是( )
A、y=
| |||||||||||
| B、y=4x2-4x+1 | |||||||||||
C、y=ln
| |||||||||||
D、y=
|
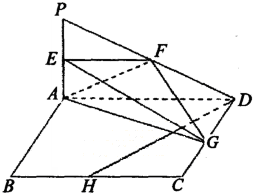 如图,四边形ABCD为正方形,PA⊥平面ABCD,且AD=2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.
如图,四边形ABCD为正方形,PA⊥平面ABCD,且AD=2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.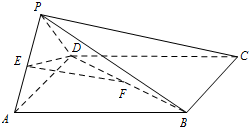 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.