题目内容
在等差数列{an}中,an=
n-
,求数列{|an|﹜的前n项和Tn.
| 3 |
| 2 |
| 21 |
| 2 |
考点:数列的求和
专题:等差数列与等比数列
分析:设等差数列{an}的前n项和为Sn,当n≤7时,Tn=-Sn,当n>7时,Tn=Sn-2S7.
解答:
解:在等差数列{an}中,an=
n-
,
∴a1=
-
=-9,a2=
×2-
=-
,d=-
+9=
,
设等差数列{an}的前n项和为Sn,
由an=
n-
≥0,得n≥7.
∴当n≤7时,Tn=-Sn=-[-9n+
×
]=9n-
=
.
当n>7时,Tn=Sn-2S7=
+252.
∴Tn=
.
| 3 |
| 2 |
| 21 |
| 2 |
∴a1=
| 3 |
| 2 |
| 21 |
| 2 |
| 3 |
| 2 |
| 21 |
| 2 |
| 15 |
| 2 |
| 15 |
| 2 |
| 3 |
| 2 |
设等差数列{an}的前n项和为Sn,
由an=
| 3 |
| 2 |
| 21 |
| 2 |
∴当n≤7时,Tn=-Sn=-[-9n+
| n(n-1) |
| 2 |
| 3 |
| 2 |
| 3n2-3n |
| 4 |
| 39n-3n2 |
| 4 |
当n>7时,Tn=Sn-2S7=
| 39n-3n2 |
| 4 |
∴Tn=
|
点评:本题考查数列的各项的绝对值的前n项和的求法,是中档题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
函数f(x)=xsinx+cosx的导函数原点处的部分图象大致为( )
A、 |
B、 |
C、 |
D、 |
函数f(x)=x3-3x2+5的单调减区间是( )
| A、(0,2) |
| B、(0,3) |
| C、(0,1) |
| D、(0,5) |
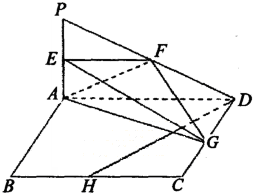 如图,四边形ABCD为正方形,PA⊥平面ABCD,且AD=2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.
如图,四边形ABCD为正方形,PA⊥平面ABCD,且AD=2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.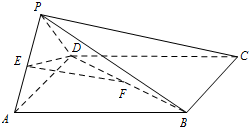 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.