题目内容
已知cosA=
，cos（A+B）=
，且A，B均为锐角，求sinB的值．
| 4 |
| 5 |
| 3 |
| 5 |
考点：两角和与差的余弦函数
专题：三角函数的求值
分析：先利用同角三角函数基本关系分别求得sinA和sin（A+B）的值，进而利用sinB=sin（A+B-A）通过两角和公式展开后求得答案．
解答：
解：∵A，B均为锐角，
∴0＜A+B＜π，
∴sinA=
=
，sin（A+B）=
=
，
∴sinB=sin（A+B-A）=sin（A+B）cosB-cos（A+B）sinB=
×
-
×
=
．
∴0＜A+B＜π，
∴sinA=
| 1-cos2A |
| 3 |
| 5 |
| 1-cos2(A+B) |
| 4 |
| 5 |
∴sinB=sin（A+B-A）=sin（A+B）cosB-cos（A+B）sinB=
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 7 |
| 25 |
点评：本题主要考查了两角和与差的正弦函数的应用．解题的关键是借助sinB=sin（A+B-A），利用两角和公式来解决问题．
练习册系列答案
相关题目
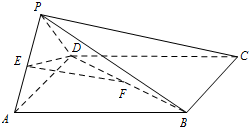如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，E，F分别为PA，BD中点，PA=PD=AD=2．
某校高一（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损，可见部分如图．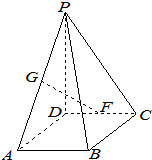
在四棱锥P-ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AB=1，BC=2，PD=