题目内容
已知函数f(x)=x2+bx+c,其中:0≤b≤2,0≤c≤2,记函数f(x)满足条件
为事件A,则事件A发生的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:我们可以以b,c为横纵坐标建立坐标系,并把0≤b≤2,0≤c≤2所表示的区域表示出来,并将
代入函数f(x)=x2+bx+x转化为一个关于b、c的不等式,画出其表示的图形,计算面积后,代入几何概型公式,即可求解.
|
解答:
 解:我们可以以b,c为横纵坐标建立坐标系,并把0≤b≤2,0≤c≤2所表示的区域表示出来,
解:我们可以以b,c为横纵坐标建立坐标系,并把0≤b≤2,0≤c≤2所表示的区域表示出来,
如图所示,其面积为4,
由于函数f(x)满足条件
,即
,亦即
.
在以b,c为横纵坐标的坐标系中,画出其表示的图形如图中阴影所示,
其面积为:
×2×2=2
所以满足条件的概率为
.
故选:D
 解:我们可以以b,c为横纵坐标建立坐标系,并把0≤b≤2,0≤c≤2所表示的区域表示出来,
解:我们可以以b,c为横纵坐标建立坐标系,并把0≤b≤2,0≤c≤2所表示的区域表示出来,如图所示,其面积为4,
由于函数f(x)满足条件
|
|
|
在以b,c为横纵坐标的坐标系中,画出其表示的图形如图中阴影所示,
其面积为:
| 1 |
| 2 |
所以满足条件的概率为
| 1 |
| 2 |
故选:D
点评:几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=
求解.
| N(A) |
| N |

练习册系列答案
相关题目
若集合A={1,m2},集合B={3,9},则“m=3”是“A∩B={9}”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )


| A、48cm3 |
| B、98cm3 |
| C、98cm3 |
| D、78cm3 |
从[0,10]中任取一个数x,从[0,6]中任取一个数y,则使|x-5|+|y-3|≤4的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
,则f(2014)的值为( )
|
A、
| ||
| B、2 | ||
C、-
| ||
| D、-2 |
设函数f(x)=(x-1)kcosx(k∈N*),则( )
| A、当k=2013时,f(x)在x=1处取得极小值 |
| B、当k=2013时,f(x)在x=1处取得极大值 |
| C、当k=2014时,f(x)在x=1处取得极小值 |
| D、当k=2014时,f(x)在x=1处取得极大值 |
 如图所示,△ABC是圆O的内接三角形,AC=BC,D为弧AB上任一点,延长DA至点E,使CE=CD.
如图所示,△ABC是圆O的内接三角形,AC=BC,D为弧AB上任一点,延长DA至点E,使CE=CD.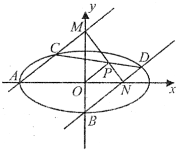 如图,过椭圆L的左顶点A(-3,0)和下顶点B且斜率均为k的两直线l1,l2分别交椭圆于C,D,又l1交y轴于M,l2交x轴于N,且CD与MN相交于点P,当k=3时,△ABM是直角三角形.
如图,过椭圆L的左顶点A(-3,0)和下顶点B且斜率均为k的两直线l1,l2分别交椭圆于C,D,又l1交y轴于M,l2交x轴于N,且CD与MN相交于点P,当k=3时,△ABM是直角三角形.