题目内容
设函数f（x）=
(x+|x|)，则函数f[f（x）]的值域为 ．
| 1 |
| 2 |
考点：函数的值域
专题：函数的性质及应用
分析：根据题意化简得f[f（x）]=
，继而求出函数值域
|
解答：
解：∵函数f（x）=
(x+|x|)，
∴f[f（x）]=
f（x）+
|f（x）|=
x+
|x|+
|
（x+|x|）|=
，
∴函数f[f（x）]的值域为[0，+∞），
故答案为：[0，+∞），
| 1 |
| 2 |
∴f[f（x）]=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
|
∴函数f[f（x）]的值域为[0，+∞），
故答案为：[0，+∞），
点评：本题考查了函数值域的求法，关键是把函数化为分段函数，属于基础题
练习册系列答案
名校课堂系列答案
相关题目
设集合M={α|α=
-
，k∈Z}，N={α|-π＜α＜π}，则M∩N等于（ ）
| kπ |
| 2 |
| π |
| 5 |
A、{-
| ||||||||
B、{-
| ||||||||
C、{-
| ||||||||
D、{
|
设全集为R，集合A={x|
≥0}，B={x|-2≤x＜0}，则（∁RA）∩B等于（ ）
| x-1 |
| x+1 |
| A、（-1，0） |
| B、[-1，0） |
| C、[-2，-1] |
| D、[-2，-1） |
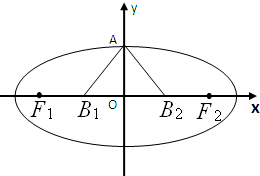如图，设椭圆C：