题目内容
已知等比数列{an}的公比q>1.a1,a3是方程x3-3x+2=0的两根.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{2n•an}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{2n•an}的前n项和Sn.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(I)由方程x2-3x+2=0,解得x=1,2,由于等比数列{an}的公比q>1.a1,a3是方程x3-3x+2=0的两根.可得a1=1,a3=2.再利用等比数列的通项公式即可得出.
(II)2n•an=2n•(
)n-1,再利用“错位相减法”、等比数列的前n项和公式即可得出.
(II)2n•an=2n•(
| 2 |
解答:
解:(I)由方程x2-3x+2=0,解得x=1,2,
∵等比数列{an}的公比q>1.a1,a3是方程x3-3x+2=0的两根.
∴a1=1,a3=2.
∴2=1×q2,
解得q=
,
∴an=(
)n-1.
(II)2n•an=2n•(
)n-1,
∴Sn=2+2×2×
+2×3×(
)2+…+2n×(
)n-1,
Sn=2
+2×2(
)2+…+2(n-1)×(
)n-1+2n(
)n,
∴(1-
)Sn=2+2[
+(
)2+…+(
)n-1]-2n(
)n=2+2×
-2n(
)n,
∴Sn=6+4
+2[(
+1)n-3-2
](
)n.
∵等比数列{an}的公比q>1.a1,a3是方程x3-3x+2=0的两根.
∴a1=1,a3=2.
∴2=1×q2,
解得q=
| 2 |
∴an=(
| 2 |
(II)2n•an=2n•(
| 2 |
∴Sn=2+2×2×
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
∴(1-
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| ||||
|
| 2 |
∴Sn=6+4
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题考查了“错位相减法”、等比数列的通项公式与前n项和公式、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知双曲线方程为x2-
=1,过P(1,2)的直线L与双曲线只有一个公共点,则L的条数共有( )
| y2 |
| 4 |
| A、4条 | B、3条 | C、2条 | D、1条 |
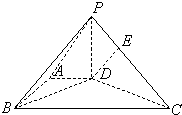 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=



