题目内容
在△ABC中,a、b、c分别是角A、B、C的对边,且满足(a+c)c=(b-a)(b+a).
(1)求角B的大小;
(2)若△ABC最大边的长为
,且sinA=2sinC,求最小边长.
(1)求角B的大小;
(2)若△ABC最大边的长为
| 14 |
考点:余弦定理,正弦定理
专题:解三角形
分析:(1)根据余弦定理即可求角B的大小;
(2)确定△ABC最大边和最小边,结合正弦定理和余弦定理建立方程关系即可求最小边长.
(2)确定△ABC最大边和最小边,结合正弦定理和余弦定理建立方程关系即可求最小边长.
解答:
解:(1)∵(a+c)c=(b-a)(b+a),
∴ac+c2=b2-a2,
即a2+c2-b2=-ac,
则cosB=
=
=-
,
则B=
;
(2)∵B=
,∴b为最大边,则b=
,
∵sinA=2sinC,
∴由正弦定理得a=2c,
则a>c,即最小边为c,
由余弦定理得b2=a2+c2-2accosB.
即14=4c2+c2-2×2c2×(-
)=7c2,
即c2=2,
则c=
.
∴ac+c2=b2-a2,
即a2+c2-b2=-ac,
则cosB=
| a2+c2-b2 |
| 2ac |
| -ac |
| 2ac |
| 1 |
| 2 |
则B=
| 2π |
| 3 |
(2)∵B=
| 2π |
| 3 |
| 14 |
∵sinA=2sinC,
∴由正弦定理得a=2c,
则a>c,即最小边为c,
由余弦定理得b2=a2+c2-2accosB.
即14=4c2+c2-2×2c2×(-
| 1 |
| 2 |
即c2=2,
则c=
| 2 |
点评:本题主要考查正弦定理和余弦定理的应用,根据条件建立方程关系是解决本题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
不等式ax2-(a+2)x+2≥0(a<0)的解集为( )
A、[
| ||
B、[1,
| ||
C、(-∞,
| ||
D、(-∞,1]∪[
|
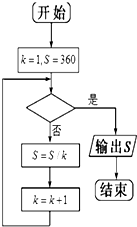 执行如图所示的程序框图,运行的结果为S=3,那么判断框中应填入的关于k的判断条件是( )
执行如图所示的程序框图,运行的结果为S=3,那么判断框中应填入的关于k的判断条件是( )| A、k>6? | B、k<6? |
| C、k>5? | D、k<5? |