题目内容
{an}是由实数构成的无穷等比数列,Sn=a1+a2+…+an,关于数列{Sn},给出下列命题:
(1)数列{Sn}中任意一项均不为0;
(2)数列{Sn}中必有一项为0;
(3)数列{Sn}中或者任意一项均不为0,或者有无穷多项为0;
(4)数列{Sn}中一定不可能出现Sn=Sn+2;
(5)数列{Sn}中一定不可能出现Sn=Sn+3;
则其中正确的命题是 .(把正确命题的序号都填上)
(1)数列{Sn}中任意一项均不为0;
(2)数列{Sn}中必有一项为0;
(3)数列{Sn}中或者任意一项均不为0,或者有无穷多项为0;
(4)数列{Sn}中一定不可能出现Sn=Sn+2;
(5)数列{Sn}中一定不可能出现Sn=Sn+3;
则其中正确的命题是
考点:命题的真假判断与应用
专题:推理和证明
分析:对于①举反例an=(-1)n即可.对于②举反例an=n即可.对于③是正确的命题,q≠1时可证Sn≠0恒成立,
q=-1时Sn有有无穷多项为0;对于④利用③的结论即可反证.对于⑤利用反证即可
q=-1时Sn有有无穷多项为0;对于④利用③的结论即可反证.对于⑤利用反证即可
解答:
解:{an}是由实数构成的无穷等比数列,Sn=a1+a2+…+an
对于①,令an=(-1)n,则n=2k时Sn=S2k=0,故结论是不正确的
对于②令an=1,则Sn=n>0恒成立,故结论不正确
对于③,当q=1时,S n=na1≠0恒成立,
当q≠1且q≠-1时,Sn=
≠0恒成立
当q=-1时,n=2k时,Sn=0,n=2k-1时,Sn=a1≠0恒成立.
综上可得结论是正确的.
对于④,由①可知结论是不正确的.
对于⑤,若Sn=Sn+3,则an+1+an+2+an+3=0,∴an(1+q+q2)=0,∵an≠0,1+q+q2≠0
可知结论是正确的.
故答案为:③④
对于①,令an=(-1)n,则n=2k时Sn=S2k=0,故结论是不正确的
对于②令an=1,则Sn=n>0恒成立,故结论不正确
对于③,当q=1时,S n=na1≠0恒成立,
当q≠1且q≠-1时,Sn=
| a1(1-qn) |
| 1-q |
当q=-1时,n=2k时,Sn=0,n=2k-1时,Sn=a1≠0恒成立.
综上可得结论是正确的.
对于④,由①可知结论是不正确的.
对于⑤,若Sn=Sn+3,则an+1+an+2+an+3=0,∴an(1+q+q2)=0,∵an≠0,1+q+q2≠0
可知结论是正确的.
故答案为:③④
点评:本题借助数列的前n项和以命题的形式考查数列的概念,属于基础题易错题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
已知tan(α+β)=
,tan(β-
)=
,则tan(α+
)的值等于( )
| 2 |
| 5 |
| π |
| 4 |
| 1 |
| 4 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={x|x2-2x-3≤0},B={-1,0,1,2,3},则A∩B=( )
| A、{-1,0,1} |
| B、{0,1,2,3,} |
| C、{-1,0,1,2,3} |
| D、{0,1,2} |
设点P为双曲线
-y2=1右支上除顶点外的任意一点,F1,F2为其两焦点,则△F1PF2的内心M在( )
| x2 |
| 4 |
| A、直线x=2上 |
| B、直线x=1上 |
| C、直线y=2x上 |
| D、直线y=x上 |
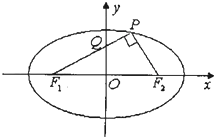 椭圆C:
椭圆C: 如图,在四棱锥E-ABCD中,四边形ABCD为矩形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥平面ACE.
如图,在四棱锥E-ABCD中,四边形ABCD为矩形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥平面ACE.