题目内容
已知集合A={x|x2-2x-3≤0},B={-1,0,1,2,3},则A∩B=( )
| A、{-1,0,1} |
| B、{0,1,2,3,} |
| C、{-1,0,1,2,3} |
| D、{0,1,2} |
考点:交集及其运算
专题:集合
分析:首先利用不等式化简集合A,然后由交集的定义解得即可.
解答:
解:∵集合A={x|x2-2x-3≤0}={x|-1≤x≤3},
B={-1,0,1,2,3},
∴A∩B={-,0,1,2,3}.
故选:C.
B={-1,0,1,2,3},
∴A∩B={-,0,1,2,3}.
故选:C.
点评:本题考查交集的求法,是基础题,解题时要注意不等式性质的合理运用.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
函数f(x)=
+lg(x+2)的定义域是( )
| 1 |
| 2-x |
| A、(-∞,-2) |
| B、(2,+∞) |
| C、(-2,2)∪(2,+∞) |
| D、(-∞,+∞) |
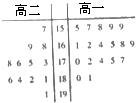 某学校为准备参加市运动会,对本校高一、高二两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm).跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下定义为“不合格”.
某学校为准备参加市运动会,对本校高一、高二两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm).跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下定义为“不合格”.