题目内容
 椭圆C:
椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 2 |
A、
| ||||
B、2-
| ||||
C、
| ||||
D、
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:首先,根据三角形的关系和焦半径公式进行处理,然后,借助于三角形之间的关系进行求解.
解答:
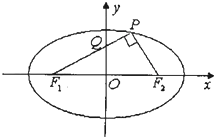
解:设点P(x0,y0),(不妨设点P位于第一象限),
由焦点半径公式,
得:|PF1|=a+ex0,|PF2|=a-ex0
∵∠F1PF2=
,
∴|PF1|2+|PF2|2=|F1F2|2
∴(a+ex0)2+(a-ex0)2=4c2
∴x0=
,
将它代入椭圆的标准方程,得
y0=
,
∴P(
,
)
∵S △OQF1:S 四边形PQOF2=1:2,
∴S △OQF1=
S△F1PF2,
∴连接QF2,
∴△OQF2≌△QF2P
∴F2P=c,
∴F1P=2a-c,∴|F1P|2+|F2P|2=|F1F2|2,
∴(2a-c)2+c2=4c2,
∴c2-2ac-2a2=0,
∴e2+2e-2=0,
∴e=
-1,e=-1-
(舍去),
∴e=
-1,
故选:C.
由焦点半径公式,
得:|PF1|=a+ex0,|PF2|=a-ex0
∵∠F1PF2=
| π |
| 2 |
∴|PF1|2+|PF2|2=|F1F2|2
∴(a+ex0)2+(a-ex0)2=4c2
∴x0=
| ||
| e |
将它代入椭圆的标准方程,得
y0=
| b2 |
| c |
∴P(
| ||
| e |
| b2 |
| c |
∵S △OQF1:S 四边形PQOF2=1:2,
∴S △OQF1=
| 1 |
| 3 |
∴连接QF2,
∴△OQF2≌△QF2P
∴F2P=c,
∴F1P=2a-c,∴|F1P|2+|F2P|2=|F1F2|2,
∴(2a-c)2+c2=4c2,
∴c2-2ac-2a2=0,
∴e2+2e-2=0,
∴e=
| 3 |
| 3 |
∴e=
| 3 |
故选:C.
点评:利用椭圆的几何性质可以求离心率时,要熟练掌握将椭圆中的某些线段长用a,b,c表示出来,例如焦点与各顶点所连线段的长,过焦点与长轴垂直的弦长等,这将有利于提高解题能力.

练习册系列答案
相关题目
函数f(x)=
+lg(x+2)的定义域是( )
| 1 |
| 2-x |
| A、(-∞,-2) |
| B、(2,+∞) |
| C、(-2,2)∪(2,+∞) |
| D、(-∞,+∞) |
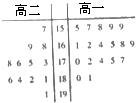 某学校为准备参加市运动会,对本校高一、高二两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm).跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下定义为“不合格”.
某学校为准备参加市运动会,对本校高一、高二两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm).跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下定义为“不合格”.