题目内容
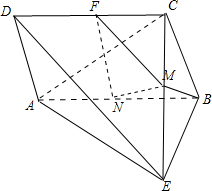
 如图,在四棱锥E-ABCD中,四边形ABCD为矩形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥平面ACE.
如图,在四棱锥E-ABCD中,四边形ABCD为矩形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥平面ACE.(Ⅰ)求证:AE⊥BC;
(Ⅱ)若点N为线段AB的中点,求证:MN∥平面ADE;
(Ⅲ)若AB=2BC,求直线AC与平面BCE所成的角.
考点:直线与平面所成的角,空间中直线与直线之间的位置关系,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)根据已知条件容易证明AE⊥平面BCE,所以得到AE⊥BC;
(Ⅱ)根据已知条件容易判断出M是CE中点,取CD中点F,并连接MF,NF,则容易说明平面MNF∥平面ADE,MN?平面MNF,所以得到MN∥平面ADE;
(Ⅲ)容易判断∠ACE是直线AC与平面BCE所成角,可设BC=1,则根据已知的边的关系可求出AE,AC,所以在Rt△ACE中可求sin∠ACE,从而求出∠ACE.
(Ⅱ)根据已知条件容易判断出M是CE中点,取CD中点F,并连接MF,NF,则容易说明平面MNF∥平面ADE,MN?平面MNF,所以得到MN∥平面ADE;
(Ⅲ)容易判断∠ACE是直线AC与平面BCE所成角,可设BC=1,则根据已知的边的关系可求出AE,AC,所以在Rt△ACE中可求sin∠ACE,从而求出∠ACE.
解答:
 解:(Ⅰ)∵BM⊥平面ACE,AE?平面ACE,∴BM⊥AE,即AE⊥BM;
解:(Ⅰ)∵BM⊥平面ACE,AE?平面ACE,∴BM⊥AE,即AE⊥BM;
又AE⊥BE,BE∩BM=B;
∴AE⊥平面BCE,BC?平面BCE,∴AE⊥BC;
(Ⅱ)取CD中点F,连接MF,NF;
BM⊥平面ACE,CE?平面ACE,∴BM⊥CE,又BE=BC;
∴M是CE的中点;
∴MF∥DE,DE?平面ADE,MF?平面ADE;
∴MF∥平面ADE,同理,NF∥平面ADE,MF∩NF=F;
∴平面MFN∥平面ADE,MN?平面MFN;
∴MN∥平面ADE;
(Ⅲ)由(Ⅰ)知AE⊥平面BCE,∴∠ACE是直线AC和平面BCE所成的角;
设BC=1,则AB=2,AB⊥BC,∴AC=
;
AE⊥BE,BE=1;
∴AE=
;
∴在Rt△ACE中,sin∠ACE=
=
=
;
∴∠ACE=acsin
.
 解:(Ⅰ)∵BM⊥平面ACE,AE?平面ACE,∴BM⊥AE,即AE⊥BM;
解:(Ⅰ)∵BM⊥平面ACE,AE?平面ACE,∴BM⊥AE,即AE⊥BM;又AE⊥BE,BE∩BM=B;
∴AE⊥平面BCE,BC?平面BCE,∴AE⊥BC;
(Ⅱ)取CD中点F,连接MF,NF;
BM⊥平面ACE,CE?平面ACE,∴BM⊥CE,又BE=BC;
∴M是CE的中点;
∴MF∥DE,DE?平面ADE,MF?平面ADE;
∴MF∥平面ADE,同理,NF∥平面ADE,MF∩NF=F;
∴平面MFN∥平面ADE,MN?平面MFN;
∴MN∥平面ADE;
(Ⅲ)由(Ⅰ)知AE⊥平面BCE,∴∠ACE是直线AC和平面BCE所成的角;
设BC=1,则AB=2,AB⊥BC,∴AC=
| 5 |
AE⊥BE,BE=1;
∴AE=
| 3 |
∴在Rt△ACE中,sin∠ACE=
| AE |
| AC |
| ||
|
| ||
| 5 |
∴∠ACE=acsin
| ||
| 5 |
点评:考查线面垂直的性质,线面垂直的判定定理,中位线的性质,线面平行的判定定理,以及面面平行的判定定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义在[0,1]上的函数f(x)满足f(0)=0,f(x)+f(1-x)=1,f(
)=
f(x),且当0≤x1<x2≤1时,f(x1)≤f(x2),则f(
)等于( )
| x |
| 5 |
| 1 |
| 2 |
| 1 |
| 2014 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知S=
•(sin
+sin
+sin
+…+sin
),则与S的值最接近的是( )
| π |
| 20000 |
| π |
| 20000 |
| 2π |
| 20000 |
| 3π |
| 20000 |
| 10000π |
| 20000 |
| A、0.99818 |
| B、0.9999 |
| C、1.0001 |
| D、2.0002 |
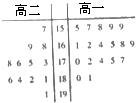 某学校为准备参加市运动会,对本校高一、高二两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm).跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下定义为“不合格”.
某学校为准备参加市运动会,对本校高一、高二两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm).跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下定义为“不合格”.