题目内容
在极坐标系中，圆ρ=2cosθ的圆心到直线ρcosθ=2的距离是 ．
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：把极坐标化为直角坐标，即可得出．
解答：
解：圆ρ=2cosθ化为ρ2=2ρcosθ，∴x2+y2=2x，化为（x-1）2+y2=1．
可得圆心P（1，0），
直线ρcosθ=2即x=2．
∴圆心P到直线的距离d=2-1=1．
故答案为：1．
可得圆心P（1，0），
直线ρcosθ=2即x=2．
∴圆心P到直线的距离d=2-1=1．
故答案为：1．
点评：本题考查了极坐标化为直角坐标，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
定义在[0，1]上的函数f（x）满足f（0）=0，f（x）+f（1-x）=1，f（
）=
f（x），且当0≤x1＜x2≤1时，f（x1）≤f（x2），则f（
）等于（ ）
| x |
| 5 |
| 1 |
| 2 |
| 1 |
| 2014 |
A、
| ||
B、
| ||
C、
| ||
D、
|
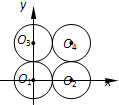如图，有4个半径都为1的圆，其圆心分别为O1（0，0），O2（2，0），O3（0，2），O4（2，2）．记集合M={⊙Oi|i=1，2，3，4}．若A，B为M的非空子集，且A中的任何一个圆与B中的任何一个圆均无公共点，则称 （A，B） 为一个“有序集合对”（当A≠B时，（A，B） 和 （B，A） 为不同的有序集合对），那么M中“有序集合对”（A，B） 的个数是（ ）已知S=
•（sin
+sin
+sin
+…+sin
），则与S的值最接近的是（ ）
| π |
| 20000 |
| π |
| 20000 |
| 2π |
| 20000 |
| 3π |
| 20000 |
| 10000π |
| 20000 |
| A、0.99818 |
| B、0.9999 |
| C、1.0001 |
| D、2.0002 |