题目内容
已知集合A={x|
≥0},B={x|2a<x≤a+1},若B⊆A,求实数a的取值范围.
| x-1 |
| x+1 |
考点:其他不等式的解法,集合的包含关系判断及应用
专题:计算题,分类讨论,不等式的解法及应用,集合
分析:分别求出A中其他不等式的解集,根据B为A的子集,对B讨论,若B=∅,若B≠∅,列出关于a的不等式,求出不等式的解集最后求并集,即可得到a的范围.
解答:
解:集合A={x|
≥0}={x|x≥1或x<-1},
由于B⊆A,
则若B=∅,即有2a≥a+1,解得a≥1;
若B≠∅,则
或
,即a<-2或
≤a<1.
综上,可得a≥
或a<-2.
故实数a的取值范围是:(-∞,-2)∪[
,+∞).
| x-1 |
| x+1 |
由于B⊆A,
则若B=∅,即有2a≥a+1,解得a≥1;
若B≠∅,则
|
|
| 1 |
| 2 |
综上,可得a≥
| 1 |
| 2 |
故实数a的取值范围是:(-∞,-2)∪[
| 1 |
| 2 |
点评:本题考查其它不等式的解法,考查集合的包含关系和运用,考查分类讨论的思想方法,属于中档题和易错题.

练习册系列答案
相关题目
已知平面上三点A,B,C满足(
+
)•
=0,则△ABC的形状是( )
| BC |
| BA |
| AC |
| A、等边三角形 |
| B、等腰三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}的子集个数是( )
| A、5 | B、8 | C、16 | D、32 |
函数f(x)=
+lg(x+2)的定义域是( )
| 1 |
| 2-x |
| A、(-∞,-2) |
| B、(2,+∞) |
| C、(-2,2)∪(2,+∞) |
| D、(-∞,+∞) |
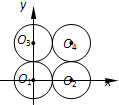 如图,有4个半径都为1的圆,其圆心分别为O1(0,0),O2(2,0),O3(0,2),O4(2,2).记集合M={⊙Oi|i=1,2,3,4}.若A,B为M的非空子集,且A中的任何一个圆与B中的任何一个圆均无公共点,则称 (A,B) 为一个“有序集合对”(当A≠B时,(A,B) 和 (B,A) 为不同的有序集合对),那么M中“有序集合对”(A,B) 的个数是( )
如图,有4个半径都为1的圆,其圆心分别为O1(0,0),O2(2,0),O3(0,2),O4(2,2).记集合M={⊙Oi|i=1,2,3,4}.若A,B为M的非空子集,且A中的任何一个圆与B中的任何一个圆均无公共点,则称 (A,B) 为一个“有序集合对”(当A≠B时,(A,B) 和 (B,A) 为不同的有序集合对),那么M中“有序集合对”(A,B) 的个数是( )