题目内容
设点P为双曲线
-y2=1右支上除顶点外的任意一点，F1，F2为其两焦点，则△F1PF2的内心M在（ ）
| x2 |
| 4 |
| A、直线x=2上 |
| B、直线x=1上 |
| C、直线y=2x上 |
| D、直线y=x上 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：充分利用平面几何图形的性质解题．因从同一点出发的切线长相等，得|PD|=|PN|，|F1N|=|F1K|，|F2K=|F2D|，再结合双曲线的定义得|F1K|-|F2K|=2a，从而即可求得△PF1F2的内心M的横坐标．
解答：
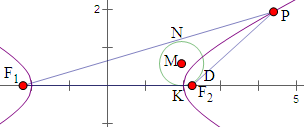解：如图△PF1F2的内切圆圆心为M，
边PF1、PF2、F1F2上的切点分别为N、D、K，
易见K、M横坐标相等，
|PD|=|PN|，|F1N|=|F1K|，|F2K=|F2D|，
由|PF1|-|PF2|=2a，
即：|PN|+|NF1|-（|PD|+|DF2|）=2a，得|NF1|-|DF2|=2a即|F1K|-|F2K|=2a，
记M的横坐标为x0，则K（x0，0），
于是：x0+c-（c-x0）=2a，
得x0=a，而a=2，
故选A
解：如图△PF1F2的内切圆圆心为M，边PF1、PF2、F1F2上的切点分别为N、D、K，
易见K、M横坐标相等，
|PD|=|PN|，|F1N|=|F1K|，|F2K=|F2D|，
由|PF1|-|PF2|=2a，
即：|PN|+|NF1|-（|PD|+|DF2|）=2a，得|NF1|-|DF2|=2a即|F1K|-|F2K|=2a，
记M的横坐标为x0，则K（x0，0），
于是：x0+c-（c-x0）=2a，
得x0=a，而a=2，
故选A
点评：本题主要考查了双曲线的定义、双曲线的应用及转化问题的能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
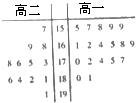某学校为准备参加市运动会，对本校高一、高二两个田径队中30名跳高运动员进行了测试，并用茎叶图表示出本次测试30人的跳高成绩（单位：cm）．跳高成绩在175cm以上（包括175cm）定义为“合格”，成绩在175cm以下定义为“不合格”．