题目内容
15．已知集合A={x|2x+2＜1}，B={x|x2-2x-3＞0}，则（∁RA）∩B=（ ）| A． | [-2，-1） | B． | （-∞，-2] | C． | [-2，-1）∪（3，+∞） | D． | （-2，-1）∪（3，+∞） |
分析 化简集合A、B，根据补集与交集的定义写出（∁RA）∩B．
解答 解：集合A={x|2x+2＜1}={x|x+2＜0}={x|x＜-2}，
B={x|x2-2x-3＞0}={x|x＜-1或x＞3}，
则∁RA={x|x≥-2}，
（∁RA）∩B={x|-2≤x＜-1或x＞3}=[-2，-1）∪（3，+∞）．
故选：C．
点评 本题考查了集合的化简与运算问题，是基础题目．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
5．若m，n∈N*则a＞b是（am-bm）•（an-bn）＞0成立的（ ）条件．
| A． | 充分非必要 | B． | 必要非充分 | ||
| C． | 充分必要 | D． | 既非充分又非必要 |
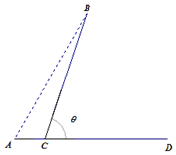某城市A计划每天从蔬菜基地B处给本市供应蔬菜，为此，准备从主干道AD的C处（不在端点A、D处）做一条道路CB，主干道AD的长为60千米，设计路线如图所示，测得蔬菜基地B在城市A的东偏北60°处，AB长为60千米，设∠BCD=θ，运输汽车在主干道AD上的平均车速为60千米/小时，在道路CB上的平均车速为20千米/小时．
10．将正奇数按如下规律填在5列的数表中：则2015排在该表的第252行，第1列．（行是从上往下数，列是从左往右数）．
| 1 | 3 | 5 | 7 | |
| 15 | 13 | 11 | 9 | |
| 17 | 19 | 21 | 23 | |
| 31 | 29 | 27 | 25 | |
| … | … | … | … | … |
如图所示，五面体ABCDFE中，AB∥CD∥EF，四边形ABCD，ABEF，CDFE都是等腰梯形，并且平面ABCD⊥平面ABEF，AB=12，CD=3，EF=4，梯形ABCD的高为3，EF到平面ABCD的距离为6，则此五面体的体积为57．