题目内容
3.将函数f(x)=Asin(ωx+ϕ)(ω>0,|ϕ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{12}$单位后得到的函数图象关于直线x=$\frac{π}{2}$对称,且平移后所得函数的单调递增区间为$(0,\frac{π}{2})$,则实数ϕ的值为$-\frac{π}{3}$.分析 根据函数y=Asin(ωx+φ)的图象变换规律得到平移后函数解析式为g(x)=Asin(ωx-$\frac{ωπ}{12}$+φ).由已知条件推知该函数的最小正周期为π,易得ω=2,然后结合正弦函数图象的对称性质来求φ的值即可.
解答 解:将函数$f(x)=Asin(ωx+ϕ)(ω>0,|ϕ|<\frac{π}{2})$的图象向右平移$\frac{π}{12}$单位后得到的函数g(x)=Asin(ωx-$\frac{ωπ}{12}$+φ).
∵函数f(x)=Asin(ωx-$\frac{ωπ}{12}$+φ)的单调递增区间为$(0,\frac{π}{2})$,
∴T=$\frac{2π}{ω}$=π,则ω=2,
又平移后得到的函数图象关于直线x=$\frac{π}{2}$对称,
∴2×$\frac{π}{2}$-$\frac{π}{6}$+φ=$\frac{π}{2}$(k∈Z),
则φ=$-\frac{π}{3}$.
故答案是:$-\frac{π}{3}$.
点评 本题主要考查正弦函数的图象的对称性,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.已知正实数x,y满足xy=1,若81x2+y2≥m恒成立,则实数m的取值范围为( )
| A. | (-∞,9] | B. | (-∞,18] | C. | [9,+∞) | D. | [18,+∞) |
15.已知集合A={x|2x+2<1},B={x|x2-2x-3>0},则(∁RA)∩B=( )
| A. | [-2,-1) | B. | (-∞,-2] | C. | [-2,-1)∪(3,+∞) | D. | (-2,-1)∪(3,+∞) |
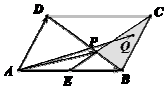 如图,在平行四边形ABCD中,点E为边AB的中点,BD与CE交于点P,若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{AD}(x,y∈R)$,则2x+y=;若点Q是△BCP内部(包括边界)一动点,且$\overrightarrow{AQ}=m\overrightarrow{AB}+n\overrightarrow{AD}(m,n∈R)$,则m+2n的取值范围为[1,3].
如图,在平行四边形ABCD中,点E为边AB的中点,BD与CE交于点P,若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{AD}(x,y∈R)$,则2x+y=;若点Q是△BCP内部(包括边界)一动点,且$\overrightarrow{AQ}=m\overrightarrow{AB}+n\overrightarrow{AD}(m,n∈R)$,则m+2n的取值范围为[1,3].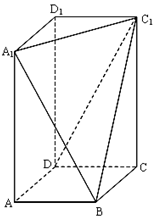 已知长方体ABCD-A1B1C1D1,其中AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后.得到如图所示的,且这个几何体的体积为$\frac{40}{3}$.
已知长方体ABCD-A1B1C1D1,其中AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后.得到如图所示的,且这个几何体的体积为$\frac{40}{3}$.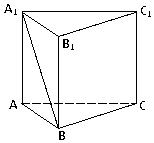 如图,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=4,∠ABC=90°;
如图,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=4,∠ABC=90°;