题目内容
20. 如图所示,五面体ABCDFE中,AB∥CD∥EF,四边形ABCD,ABEF,CDFE都是等腰梯形,并且平面ABCD⊥平面ABEF,AB=12,CD=3,EF=4,梯形ABCD的高为3,EF到平面ABCD的距离为6,则此五面体的体积为57.
如图所示,五面体ABCDFE中,AB∥CD∥EF,四边形ABCD,ABEF,CDFE都是等腰梯形,并且平面ABCD⊥平面ABEF,AB=12,CD=3,EF=4,梯形ABCD的高为3,EF到平面ABCD的距离为6,则此五面体的体积为57.
分析 连结DE、BD,此五面体的体积为V=VD-ABEF+VE-BDC,由此能求出结果.
解答 解:∵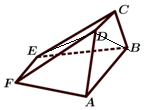 五面体ABCDFE中,AB∥CD∥EF,四边形ABCD,ABEF,CDFE都是等腰梯形,
五面体ABCDFE中,AB∥CD∥EF,四边形ABCD,ABEF,CDFE都是等腰梯形,
平面ABCD⊥平面ABEF,AB=12,CD=3,EF=4,梯形ABCD的高为3,EF到平面ABCD的距离为6,
∴S梯形ABEF=$\frac{1}{2}(4+12)×6$=48,
S△BCD=$\frac{1}{2}×3×3$=$\frac{9}{2}$,
连结DE、BD,
∴此五面体的体积为:
V=VD-ABEF+VE-BDC
=$\frac{1}{3}×{S}_{梯形ABEF}×3+\frac{1}{3}×{S}_{△BCD}×3$
=$\frac{1}{3}×48×3+\frac{1}{3}×\frac{9}{2}×6$
=57.
故答案为:57.
点评 本题考查五面体的体积的求法,是中档题,解题时要认真审题,注意等体积法的合理运用.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
11.已知正实数x,y满足xy=1,若81x2+y2≥m恒成立,则实数m的取值范围为( )
| A. | (-∞,9] | B. | (-∞,18] | C. | [9,+∞) | D. | [18,+∞) |
15.已知集合A={x|2x+2<1},B={x|x2-2x-3>0},则(∁RA)∩B=( )
| A. | [-2,-1) | B. | (-∞,-2] | C. | [-2,-1)∪(3,+∞) | D. | (-2,-1)∪(3,+∞) |
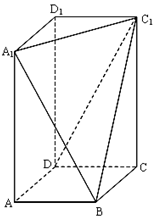 已知长方体ABCD-A1B1C1D1,其中AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后.得到如图所示的,且这个几何体的体积为$\frac{40}{3}$.
已知长方体ABCD-A1B1C1D1,其中AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后.得到如图所示的,且这个几何体的体积为$\frac{40}{3}$.