题目内容
已知函数f(x)=sin(x+
)sin(x+
).
(1)求f(x)的最小正周期;
(2)若g(x)=f(x)-
,求g(x)在区间[0,
]上的值域.
| π |
| 3 |
| π |
| 2 |
(1)求f(x)的最小正周期;
(2)若g(x)=f(x)-
| ||
| 4 |
| π |
| 2 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)由三角函数中的恒等变换应用化简函数解析式可得f(x)=
sin(2x+
)+
,由正弦函数的周期公式即可求得f(x)的最小正周期;
(2)由题意可求g(x)=
sin(2x+
),由0≤x≤
,可解得-
≤
sin(2x+
)≤
,即可得解.
| 1 |
| 2 |
| π |
| 3 |
| ||
| 4 |
(2)由题意可求g(x)=
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
解答:
解:f(x)=(
sinx+
cosx)cosx …(2分)
=
sinxcosx+
cos2x
=
sin2x+
(1+cos2x) …(4分)
=
sin(2x+
)+
; …(6分)
(1)所以T=
=π. …(8分)
(2)g(x)=
sin(2x+
),
因为0≤x≤
,所以
≤2x+
≤
,
所以-
≤sin(2x+
)≤1,
可得:-
≤
sin(2x+
)≤
,
所以g(x)在区间[0,
]上的值域为[-
,
].…(12分)
| 1 |
| 2 |
| ||
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
=
| 1 |
| 4 |
| ||
| 4 |
=
| 1 |
| 2 |
| π |
| 3 |
| ||
| 4 |
(1)所以T=
| 2π |
| 2 |
(2)g(x)=
| 1 |
| 2 |
| π |
| 3 |
因为0≤x≤
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
所以-
| ||
| 2 |
| π |
| 3 |
可得:-
| ||
| 4 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
所以g(x)在区间[0,
| π |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
点评:本题主要考查了三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
相关题目
设a=log23.9,b=log20.7,c=2,则( )
| A、b<a<c |
| B、a<b<c |
| C、c<a<b |
| D、c<b<a |
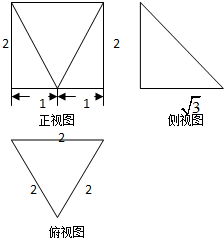 一个几何体的三视图如图所示,该几何体外接球的表面积为( )
一个几何体的三视图如图所示,该几何体外接球的表面积为( )| A、9π | ||
B、
| ||
| C、8π | ||
| D、7π |
已知在△ABC中,D是AB边上的一点,
=λ(
+
),|
|=2,|
|=1,若
=
,
=
,则用
,
表示
为( )
| CD |
| ||
|
|
| ||
|
|
| CA |
| CB |
| CA |
| b |
| CB |
| a |
| a |
| b |
| CD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
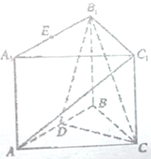 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,D是AB的中点.