题目内容
已知函数f(x)=cos(x-
),g(x)=ex•f′(x),其中e为自然对数的底数.
(Ⅰ)求曲线y=g(x)在点(0,g(0))处的切线方程;
(Ⅱ)若对任意x∈[-
,0],不等式g(x)≥x•f(x)+m恒成立,求实数m的取值范围;
(Ⅲ)试探究当x∈[
,
]时,方程g(x)=x•f(x)的解的个数,并说明理由.
| π |
| 2 |
(Ⅰ)求曲线y=g(x)在点(0,g(0))处的切线方程;
(Ⅱ)若对任意x∈[-
| π |
| 2 |
(Ⅲ)试探究当x∈[
| π |
| 4 |
| π |
| 2 |
考点:利用导数求闭区间上函数的最值,函数的零点与方程根的关系,利用导数研究曲线上某点切线方程
专题:计算题,函数的性质及应用,导数的概念及应用,导数的综合应用
分析:(Ⅰ)化简f(x)=sinx,g(x)=excosx,g(0)=e0cos0=1;从而由导数的几何意义写出切线方程;
(Ⅱ)对任意x∈[-
,0],不等式g(x)≥x•f(x)+m恒成立可化为m≤[g(x)-x•f(x)]min,x∈[-
,0],从而设h(x)=g(x)-x•f(x),x∈[-
,0],转化为函数的最值问题求解.
(Ⅲ)设H(x)=g(x)-x•f(x),x∈[
,
];从而由函数的单调性及函数零点的判定定理求解函数的零点的个数.
(Ⅱ)对任意x∈[-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
(Ⅲ)设H(x)=g(x)-x•f(x),x∈[
| π |
| 4 |
| π |
| 2 |
解答:
解:(Ⅰ)由题意得,
f(x)=sinx,g(x)=excosx,g(0)=e0cos0=1;
g′(x)=ex(cosx-sinx),g′(0)=1;
故曲线y=g(x)在点(0,g(0))处的切线方程为y=x+1;
(Ⅱ)对任意x∈[-
,0],不等式g(x)≥x•f(x)+m恒成立可化为
m≤[g(x)-x•f(x)]min,x∈[-
,0],
设h(x)=g(x)-x•f(x),x∈[-
,0],
则h′(x)=ex(cosx-sinx)-sinx-xcosx=(ex-x)cosx-(ex+1)sinx,
∵x∈[-
,0],
∴(ex-x)cosx≥0,(ex+1)sinx≤0;
故h′(x)≥0,
故h(x)在[-
,0]上单调递增,
故当x=-
时,hmin(x)=h(-
)=-
;
故m≤-
;
(Ⅲ)设H(x)=g(x)-x•f(x),x∈[
,
];
则当x∈[
,
]时,
H′(x)=ex(cosx-sinx)-sinx-xcosx=(ex-x)cosx-(ex+1)sinx<0,
故H(x)在[
,
]上单调递减,
故函数H(x)在[
,
]上至多有一个零点;
又H(
)=
(e
-
)>0,
H(
)=-
<0;
且H(x)在[
,
]上是连续不断的,
故函数H(x)在[
,
]上有且只有一个零点.
f(x)=sinx,g(x)=excosx,g(0)=e0cos0=1;
g′(x)=ex(cosx-sinx),g′(0)=1;
故曲线y=g(x)在点(0,g(0))处的切线方程为y=x+1;
(Ⅱ)对任意x∈[-
| π |
| 2 |
m≤[g(x)-x•f(x)]min,x∈[-
| π |
| 2 |
设h(x)=g(x)-x•f(x),x∈[-
| π |
| 2 |
则h′(x)=ex(cosx-sinx)-sinx-xcosx=(ex-x)cosx-(ex+1)sinx,
∵x∈[-
| π |
| 2 |
∴(ex-x)cosx≥0,(ex+1)sinx≤0;
故h′(x)≥0,
故h(x)在[-
| π |
| 2 |
故当x=-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故m≤-
| π |
| 2 |
(Ⅲ)设H(x)=g(x)-x•f(x),x∈[
| π |
| 4 |
| π |
| 2 |
则当x∈[
| π |
| 4 |
| π |
| 2 |
H′(x)=ex(cosx-sinx)-sinx-xcosx=(ex-x)cosx-(ex+1)sinx<0,
故H(x)在[
| π |
| 4 |
| π |
| 2 |
故函数H(x)在[
| π |
| 4 |
| π |
| 2 |
又H(
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
H(
| π |
| 2 |
| π |
| 2 |
且H(x)在[
| π |
| 4 |
| π |
| 2 |
故函数H(x)在[
| π |
| 4 |
| π |
| 2 |
点评:本题考查了导数的几何意义的应用及导数的综合应用,同时考查了恒成立问题及函数的最值问题,还考查了零点的个数的判断,属于难题.

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
“x>1”是“ln(ex+1)>1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、非充分非必要条件 |
已知D为△ABC的边BC的中点,△ABC所在平面内有一个点P,满足
=
+
,则
的值为( )
| PA |
| PB |
| PC |
|
| ||
|
|
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
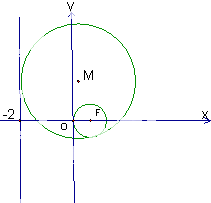 已知:动圆M与圆F:(x-1)2+y2=1内切,且与直线l:x=-2相切,动圆圆心 M的轨迹为曲线Γ
已知:动圆M与圆F:(x-1)2+y2=1内切,且与直线l:x=-2相切,动圆圆心 M的轨迹为曲线Γ