题目内容
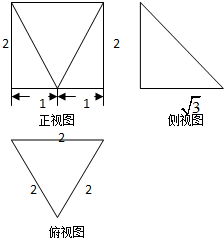 一个几何体的三视图如图所示,该几何体外接球的表面积为( )
一个几何体的三视图如图所示,该几何体外接球的表面积为( )| A、9π | ||
B、
| ||
| C、8π | ||
| D、7π |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知中的三视图可得,该几何体是一个以正视图为底面的四棱锥,其外接球,与以俯视图为底面,以2为高的正三棱柱的外接球相同,进而可得该几何体外接球的表面积.
解答:
解:由已知中的三视图可得,该几何体是一个以正视图为底面的四棱锥,
其外接球,与以俯视图为底面,以2为高的正三棱柱的外接球相同,
如图所示:
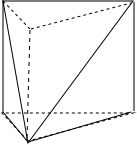
由底面边长为2,可得底面外接圆的半径为:
,
由棱柱高为2,可得球心距为1,
故外接球半径为:
=
,
故外接球的表面积S=4πr2=
π,
故选:B
其外接球,与以俯视图为底面,以2为高的正三棱柱的外接球相同,
如图所示:

由底面边长为2,可得底面外接圆的半径为:
2
| ||
| 3 |
由棱柱高为2,可得球心距为1,
故外接球半径为:
12+(
|
| ||
| 3 |
故外接球的表面积S=4πr2=
| 28 |
| 3 |
故选:B
点评:本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图所示,程序框图算法流程图的输出结果s的值为( )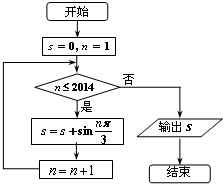

A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知△ABC中,设角A,B,C所对的边分别为a,b,c,G为△ABC的重心,且a
+b
+c
=
,则△ABC为
( )
| GA |
| GB |
| GC |
| 0 |
( )
| A、等腰直角三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等边三角形 |

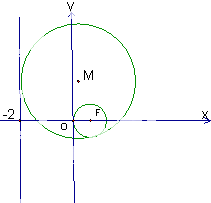 已知:动圆M与圆F:(x-1)2+y2=1内切,且与直线l:x=-2相切,动圆圆心 M的轨迹为曲线Γ
已知:动圆M与圆F:(x-1)2+y2=1内切,且与直线l:x=-2相切,动圆圆心 M的轨迹为曲线Γ