题目内容

设a=log23.9，b=log20.7，c=2，则（　　）
A、b＜a＜c
B、a＜b＜c
C、c＜a＜b
D、c＜b＜a
考点：对数值大小的比较
专题：函数的性质及应用
分析：利用指数与对数的运算性质即可得出．
解答： 解：∵0＜a=log23.9＜log24=2，b=log20.7＜0，c=2，
∴b＜a＜c．
故选：A．
点评：本题考查了指数与对数的运算性质，属于基础题．
练习册系列答案
相关题目
在正三棱锥S-ABC中，M、N分别为SC、BC的中点，且MN⊥AM，若侧棱SA=4，则正三棱锥S-ABC的外接球的表面积是（　　）
A、36πB、72π
C、144πD、48π
已知函数f（x），（x∈D），若同时满足以下条件：
①f（x）在D上单调递减或单调递增；
②存在区间[a，b]⊆D，使f（x）在[a，b]上的值域是[a，b]（a＜b）．那么撑f（x）（x∈D）为闭函数．
（1）求闭函数f（x）=
x
符合条件②的区间[a，b]；
（2）判断函数y=lnx+3x-6是不是闭函数，若是请找出区间[a，b]，若不是请说明理由；
（3）若y=（x-k）2，x∈（k，+∞）是闭函数，求实数k的取值范围．
解方程
15
27-λ
+
16
36-λ
=1．
“x＞1”是“ln（ex+1）＞1”的（　　）
A、充分不必要条件
B、必要不充分条件
C、充分必要条件
D、非充分非必要条件
已知函数f（x）=2sin2（x+
π
4
）-
3
cos2x-1，x∈[
π
4
，
π
2
]．
（1）求f（x）的单调递增区间；
（2）若存在x∈[
π
4
，
π
2
]，使得f（x）＜m成立，求实数m的取值范围．
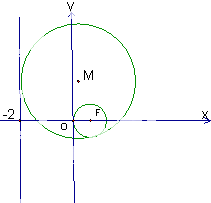已知：动圆M与圆F：（x-1）2+y2=1内切，且与直线l：x=-2相切，动圆圆心 M的轨迹为曲线Γ
（1）求曲线Γ的方程；
（2）过曲线Γ上的点 P（x0，2）引斜率分别为k1，k2的两条直线l1、l2，直线l1、l2与曲线Γ的异于点P的另一个交点分别为A、B，若k1k2=4，试探究：直线AB是否恒过定点？若恒过定点，请求出该定点的坐标，若不恒过定点，请说明理由．
已知函数f（x）=sin（x+
π
3
）sin（x+
π
2
）．
（1）求f（x）的最小正周期；
（2）若g（x）=f（x）-
3
4
，求g（x）在区间[0，
π
2
]上的值域．
如图，已知长方体ABCD-A1B1C1D1的对角线A1C与侧棱BB1所成的角为45°，且AB=BC=1，求A1C与侧面BB1C1C所成角的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网