题目内容
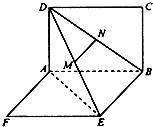如图，两矩形ABCD、ABEF所在平面互相垂直，DE与平面ABCD及平面ABEF所成角分别为30°、45°，M、N分别为DE与DB的中点，且MN=1．线段AB的长为考点：点、线、面间的距离计算
专题：空间位置关系与距离,空间角
分析：首先根据面面垂直的性质定理得到：线面垂直和线线垂直．进一步利用线面的夹角和勾股定理求的结果．
解答：
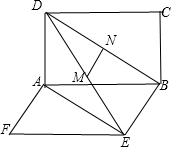解：∵两矩形ABCD、ABEF所在平面互相垂直，
∴BE⊥平面ABCD，AD⊥平面ABEF
∴BE⊥BD，AD⊥AE
∵M、N分别为DE与DB的中点，且MN=1
则：BE=4
∵DE与平面ABCD及平面ABEF所成角分别为30°、45°
∴∠EDB=30°，∠ADE=45°
在Rt△EBD中解得：DE=8．
在Rt△ADE中解得：AE=4
进一步利用勾股定理：AE2=BE2+AB2
解得：AB=4
故答案为：4
解：∵两矩形ABCD、ABEF所在平面互相垂直，∴BE⊥平面ABCD，AD⊥平面ABEF
∴BE⊥BD，AD⊥AE
∵M、N分别为DE与DB的中点，且MN=1
则：BE=4
∵DE与平面ABCD及平面ABEF所成角分别为30°、45°
∴∠EDB=30°，∠ADE=45°
在Rt△EBD中解得：DE=8．
在Rt△ADE中解得：AE=4
| 2 |
进一步利用勾股定理：AE2=BE2+AB2
解得：AB=4
故答案为：4
点评：本题考查的知识要点：面面垂直的性质定理，线面的夹角的应用，勾股定理得应用．
练习册系列答案
相关题目
i是虚数单位，复数
=（ ）
| 2-3i |
| 1-2i |
A、
| ||
B、
| ||
C、
| ||
D、
|
设-5＜a＜5，集合M={x∈N|2x-（a+5）x-10=0}．若M≠?，则满足条件的所有实数a的和等于（ ）
A、-
| ||
B、-
| ||
C、
| ||
| D、4 |
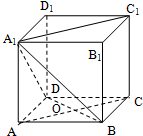如图，在棱长为a的正方体 ABCD-A1B1C1D1 中，AC 与BD相交于点O．
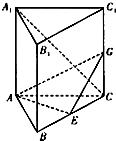如图，在直三棱柱ABC-A1B1C1中，∠BAC=90°，AC=AB=AA1，E是BC的中点．