题目内容
设a，b，c是△ABC的边长，设l是△ABC的内心，求
+
+
的值．
| |IA|2 |
| bc |
| |IB|2 |
| ca |
| |IC|2 |
| ab |
考点：函数的值
专题：计算题,作图题,解三角形
分析：由题意，
r（a+b+c）=
bcsinA，从而求出r=
，进而表示出
=
=
=
，从而求
+
+
的值．
| 1 |
| 2 |
| 1 |
| 2 |
| bcsinA |
| a+b+c |
| |IA|2 |
| bc |
4bccos2
| ||
| (a+b+c)2 |
| 2bc(1+cosA) |
| (a+b+c)2 |
| b2+c2-a2+2bc |
| (a+b+c)2 |
| |IA|2 |
| bc |
| |IB|2 |
| ca |
| |IC|2 |
| ab |
解答：
解：如图：∵l是△ABC的内心，设l到三边的距离为r，
∴
r（a+b+c）=
bcsinA，
∴r=
，
∴|lA|2=（
•
）2，
∴
=
=
=
，
∴
+
+
=
+
+
=
=1．
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴r=
| bcsinA |
| a+b+c |
∴|lA|2=（
| bcsinA |
| a+b+c |
| 1 | ||
sin
|
∴
| |IA|2 |
| bc |
4bccos2
| ||
| (a+b+c)2 |
| 2bc(1+cosA) |
| (a+b+c)2 |
| b2+c2-a2+2bc |
| (a+b+c)2 |
∴
| |IA|2 |
| bc |
| |IB|2 |
| ca |
| |IC|2 |
| ab |
| b2+c2-a2+2bc |
| (a+b+c)2 |
| c2+a2-b2+2ac |
| (a+b+c)2 |
| a2+b2-c2+2ab |
| (a+b+c)2 |
| (a+b+c)2 |
| (a+b+c)2 |
点评：本题考查了解三角形及三角函数的应用，属于中档题．
练习册系列答案
相关题目
已知实数x，y满足
，若（-1，0）是使mx+y取得最大值的可行解，则实数m的取值范围是（ ）
|
| A、m≤3 | ||
| B、m≤-3 | ||
C、m≥-
| ||
D、m≥
|
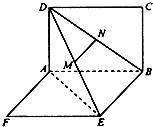如图，两矩形ABCD、ABEF所在平面互相垂直，DE与平面ABCD及平面ABEF所成角分别为30°、45°，M、N分别为DE与DB的中点，且MN=1．线段AB的长为