题目内容
设函数f(x)=lnx-x2+ax(a∈R).
(Ⅰ) 求函数f(x)的单调区间;
(Ⅱ) 已知A(x1,f(x1)),B(x2,f(x2))(x1≠x2)是函数f(x)在x∈[1,+∞)的图象上的任意两点,且满足
<2,求a的最大值;
(Ⅲ) 设g(x)=xe1-x,若对于任意给定的x0∈(0,e],方程f(x)+1=g(x0)在(0,e]内有两个不同的实数根,求a的取值范围.(其中e是自然对数的底数)
(Ⅰ) 求函数f(x)的单调区间;
(Ⅱ) 已知A(x1,f(x1)),B(x2,f(x2))(x1≠x2)是函数f(x)在x∈[1,+∞)的图象上的任意两点,且满足
| f(x1)-f(x2) |
| x1-x2 |
(Ⅲ) 设g(x)=xe1-x,若对于任意给定的x0∈(0,e],方程f(x)+1=g(x0)在(0,e]内有两个不同的实数根,求a的取值范围.(其中e是自然对数的底数)
考点:导数在最大值、最小值问题中的应用
专题:导数的概念及应用,导数的综合应用
分析:(1)直接对原函数求导,令导数大于0,解得增区间,令导数小于0,解得减区间;
(2)因为是不等式恒成立,因此将原式转化为函数的最值问题,通过变形构造出函数φ(x)=f(x)-2x,通过研究该函数的单调性,进而转化为该函数的导数小于等于0恒成立,最终使问题获得解答;
(3)其实还是要数形结合,两个函数构造的方程在某一区间上有两个根,即它们的图象有两个公共点,结合单调性进行分析,容易使问题获得解答.
(2)因为是不等式恒成立,因此将原式转化为函数的最值问题,通过变形构造出函数φ(x)=f(x)-2x,通过研究该函数的单调性,进而转化为该函数的导数小于等于0恒成立,最终使问题获得解答;
(3)其实还是要数形结合,两个函数构造的方程在某一区间上有两个根,即它们的图象有两个公共点,结合单调性进行分析,容易使问题获得解答.
解答:
解:(Ⅰ) f′(x)=
-2x+a=
,
由f'(x)=0,得-2x2+ax+1=0,该方程的判别式△=a2+8>0,
可知方程-2x2+ax+1=0有两个实数根
,又x>0,故取x=
,
当x∈(0,
)时,f'(x)>0,函数f(x)单调递增;当x∈(
,+∞)时,f'(x)<0,函数f(x)单调递减.
则函数f(x)的单调递增区间是(0,
);递减区间是(
,+∞).
(Ⅱ)不妨设x1>x2≥1,不等式
<2转化为f(x1)-2x1<f(x2)-2x2,
令φ(x)=f(x)-2x,可知函数φ(x)在区间[1,+∞)上单调递减,故φ'(x)=f'(x)-2≤0恒成立,
故
-2x+a-2≤0恒成立,即a≤2x-
+2恒成立.
当x∈[1,+∞)时,函数y=2x-
+2单调递增,故当x=1时,函数y=2x-
+2取得最小值3,则实数a的取值范围是a≤3,则实数a的最大值为3.
(Ⅲ)g'(x)=(1-x)e1-x,当x∈(0,1)时,g'(x)>0,g(x)是增函数;当x∈(1,e)时,g'(x)<0,g(x)是减函数.可得函数g(x)在区间(0,e]的值域为(0,1].
令F(x)=f(x)+1,则F′(x)=f′(x)=
,
由F'(x)=0,结合(Ⅰ)可知,方程F'(x)=0在(0,∞)上有一个实数根x3,若x3≥e,则F(x)在(0,e]上单调递增,不合题意,
可知F'(x)=0在(0,e]有唯一的解x3=
,且F(x)在(0,
)上单调递增;在(
,+∞)上单调递减.
因为?x0∈(0,e],方程f(x)+1=g(x0)在(0,e]内有两个不同的实数根,所以F(e)≤0,且F(x)max>1.
由F(e)≤0,即lne-e2+ae+1≤0,解得a≤e-
.
由F(x)max=f(x3)+1>1,即lnx3-
+ax3+1>1,lnx3-
+ax3>0,
因为-2
+ax3+1=0,所以a=2x3-
,代入lnx3-
+ax3>0,得lnx3+
-1>0,
令h(x)=lnx+x2-1,可知函数h(x)在(0,e]上单调递增,而h(1)=0,则h(x3)>h(1)=0,
所以1<x3<e,而a=2x3-
在1<x3<e时单调递增,可得1<a<2e-
,
综上所述,实数a的取值范围是(1,e-
].
| 1 |
| x |
| -2x2+ax+1 |
| x |
由f'(x)=0,得-2x2+ax+1=0,该方程的判别式△=a2+8>0,
可知方程-2x2+ax+1=0有两个实数根
a±
| ||
| 4 |
a+
| ||
| 4 |
当x∈(0,
a+
| ||
| 4 |
a+
| ||
| 4 |
则函数f(x)的单调递增区间是(0,
a+
| ||
| 4 |
a+
| ||
| 4 |
(Ⅱ)不妨设x1>x2≥1,不等式
| f(x1)-f(x2) |
| x1-x2 |
令φ(x)=f(x)-2x,可知函数φ(x)在区间[1,+∞)上单调递减,故φ'(x)=f'(x)-2≤0恒成立,
故
| 1 |
| x |
| 1 |
| x |
当x∈[1,+∞)时,函数y=2x-
| 1 |
| x |
| 1 |
| x |
(Ⅲ)g'(x)=(1-x)e1-x,当x∈(0,1)时,g'(x)>0,g(x)是增函数;当x∈(1,e)时,g'(x)<0,g(x)是减函数.可得函数g(x)在区间(0,e]的值域为(0,1].
令F(x)=f(x)+1,则F′(x)=f′(x)=
| -2x2+ax+1 |
| x |
由F'(x)=0,结合(Ⅰ)可知,方程F'(x)=0在(0,∞)上有一个实数根x3,若x3≥e,则F(x)在(0,e]上单调递增,不合题意,
可知F'(x)=0在(0,e]有唯一的解x3=
a+
| ||
| 4 |
a+
| ||
| 4 |
a+
| ||
| 4 |
因为?x0∈(0,e],方程f(x)+1=g(x0)在(0,e]内有两个不同的实数根,所以F(e)≤0,且F(x)max>1.
由F(e)≤0,即lne-e2+ae+1≤0,解得a≤e-
| 2 |
| e |
由F(x)max=f(x3)+1>1,即lnx3-
| x | 2 3 |
| x | 2 3 |
因为-2
| x | 2 3 |
| 1 |
| x3 |
| x | 2 3 |
| x | 2 3 |
令h(x)=lnx+x2-1,可知函数h(x)在(0,e]上单调递增,而h(1)=0,则h(x3)>h(1)=0,
所以1<x3<e,而a=2x3-
| 1 |
| x3 |
| 1 |
| e |
综上所述,实数a的取值范围是(1,e-
| 2 |
| e |
点评:本题综合考查了利用导数研究函数的单调性、零点的存在性问题以及不等式的恒成立问题,属于压轴题,要仔细体会其解题思想.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
i是虚数单位,计算
+
=( )
| 1-i |
| 1+i |
| 1+i |
| 1-i |
| A、-2i | B、0 | C、1 | D、2i |
我国的人口普查每十年进行一次,在第五次(2000年11月1日开始)人口普查时我国人口约为13亿,并发现我国人口的年平均增长率约为1%,如果按照这种速度增长,在我国开始第七次(2020年11月1日开始)普查时的人口数约为( )亿.
| A、13(1+20×1%) |
| B、13(1+19×1%) |
| C、13(1+1%)20 |
| D、13(1+1%)19 |
已知四面体的各条棱长均为2,则它的表面积是( )
A、
| ||
B、2
| ||
C、4
| ||
D、8
|
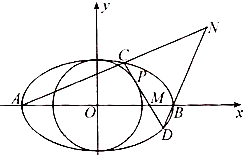 已知椭圆C1:
已知椭圆C1: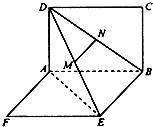 如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1.线段AB的长为
如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1.线段AB的长为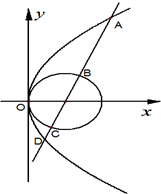 如图,抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点的直线l
如图,抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点的直线l