题目内容
求证:方程[x]+[2x]+[4x]+[8x]+[16x]+[32x]=12345无实数解.
考点:反证法与放缩法
专题:证明题,反证法
分析:利用反证法,假设方程有实数解x=n+a,其中n属于Z,0≤a<1,代入原方程化简、变形,得[2a]+[4a]+[8a]+[16a]+[32a]=12345-63n,可得195.04≤n≤195.95,而这样的整数n不存在,故原方程无实数解.
解答:
证明:假设方程有实数解x=n+a,其中n属于Z,0≤a<1,于是,
[x]=n
[2x]=2n+[2a]
[4x]=4n+[4a]
[8x]=8n+[8a]
[16x]=16n+[16a]
[32x]=32n+[32a]
代入原方程化简、变形,得
[2a]+[4a]+[8a]+[16a]+[32a]=12345-63n
由于0≤a<1,因而0≤[ka]≤k-1
故0≤12345-63n≤1+3+7+15+31=57
∴195.04≤n≤195.95
而这样的整数n不存在,
故原方程无实数解.
[x]=n
[2x]=2n+[2a]
[4x]=4n+[4a]
[8x]=8n+[8a]
[16x]=16n+[16a]
[32x]=32n+[32a]
代入原方程化简、变形,得
[2a]+[4a]+[8a]+[16a]+[32a]=12345-63n
由于0≤a<1,因而0≤[ka]≤k-1
故0≤12345-63n≤1+3+7+15+31=57
∴195.04≤n≤195.95
而这样的整数n不存在,
故原方程无实数解.
点评:本题考查反证法,考查学生分析解决问题的能力,正确运用反证法的步骤是关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
已知四面体的各条棱长均为2,则它的表面积是( )
A、
| ||
B、2
| ||
C、4
| ||
D、8
|
直线3x-4y+6=0与圆(x-2)2+(y-3)2=4的位置关系是( )
| A、直线与圆相交且过圆心 |
| B、直线与圆相交但不过圆心 |
| C、相切 |
| D、相离 |
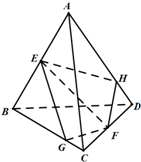 如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,有下列三个结论,其中正确的个数是( )
如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,有下列三个结论,其中正确的个数是( )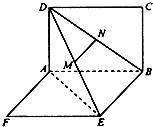 如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1.线段AB的长为
如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1.线段AB的长为