题目内容
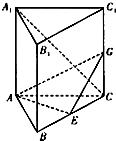 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AC=AB=AA1,E是BC的中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AC=AB=AA1,E是BC的中点.(1)求异面直线AE与A1C所成的角;
(2)若G为C1C上一点,且EG⊥A1C,试确定点G的位置;
(3)在(2)的条件下,求二面角C-AG-E的正切值.
考点:二面角的平面角及求法,异面直线及其所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(1)取B1C1的中点E1,连A1E1,E1C,可得∠E1A1C是异面直线A与A1C所成的角,利用余弦定理,即可求异面直线AE与A1C所成的角;
(2)利用△E1CC1∽△GEC,即可确定点G的位置;
(3)连结AG,设P是AC的中点,过点P作PQ⊥AG于Q,连EP,EQ,则EP⊥AC,可得∠PQE是二面角C-AG-E的平面角,即可求二面角C-AG-E的正切值.
(2)利用△E1CC1∽△GEC,即可确定点G的位置;
(3)连结AG,设P是AC的中点,过点P作PQ⊥AG于Q,连EP,EQ,则EP⊥AC,可得∠PQE是二面角C-AG-E的平面角,即可求二面角C-AG-E的正切值.
解答:
 解:(1)取B1C1的中点E1,连A1E1,E1C,
解:(1)取B1C1的中点E1,连A1E1,E1C,
则AE∥A1E1,∴∠E1A1C是异面直线A与A1C所成的角.
设AC=AB=AA1=2a,
则A1E1=
a,A1C=2
a,E1C1=
a,
∴E1C=
a,
△A1E1C中,cos∠E1A1C=
=
,
∴异面直线AE与A1C所成的角为
.
(2)由(1)知,A1E1⊥B1C1,
又∵三棱柱ABC-A1B1C1是直三棱柱∴A1E1⊥BCC1B1,
又∵EG⊥A1C,∴CE1⊥EG.
∴∠E1CC1=∠GEC,
∴△E1CC1∽△GEC,
∴
=
即
=
得CG=a,
∴G是CC1的中点;
(3)连结AG,设P是AC的中点,过点P作PQ⊥AG于Q,连EP,EQ,则EP⊥AC.
又∵平面ABC⊥平面ACC1A1,∴EP⊥平面ACC1A1
而PQ⊥AG∴EQ⊥AG.∴∠PQE是二面角C-AG-E的平面角.
由EP=a,AP=a,PQ=
,得tan∠PQE=
=
∴二面角C-AG-E的平面角正切值是
.
 解:(1)取B1C1的中点E1,连A1E1,E1C,
解:(1)取B1C1的中点E1,连A1E1,E1C,则AE∥A1E1,∴∠E1A1C是异面直线A与A1C所成的角.
设AC=AB=AA1=2a,
则A1E1=
| 2 |
| 2 |
| 2 |
∴E1C=
| 6 |
△A1E1C中,cos∠E1A1C=
| 2a2+8a2-6a2 | ||||
2×
|
| 1 |
| 2 |
∴异面直线AE与A1C所成的角为
| π |
| 3 |
(2)由(1)知,A1E1⊥B1C1,
又∵三棱柱ABC-A1B1C1是直三棱柱∴A1E1⊥BCC1B1,
又∵EG⊥A1C,∴CE1⊥EG.
∴∠E1CC1=∠GEC,
∴△E1CC1∽△GEC,
∴
| CG |
| CE |
| C1E1 |
| C1C |
| CG | ||
|
| ||
| 2a |
∴G是CC1的中点;
(3)连结AG,设P是AC的中点,过点P作PQ⊥AG于Q,连EP,EQ,则EP⊥AC.
又∵平面ABC⊥平面ACC1A1,∴EP⊥平面ACC1A1
而PQ⊥AG∴EQ⊥AG.∴∠PQE是二面角C-AG-E的平面角.
由EP=a,AP=a,PQ=
| a | ||
|
| PE |
| PQ |
| 5 |
∴二面角C-AG-E的平面角正切值是
| 5 |
点评:本题考查空间角,考查学生分析解决问题的能力,考查余弦定理的运用,正确找出空间角是关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
直线3x-4y+6=0与圆(x-2)2+(y-3)2=4的位置关系是( )
| A、直线与圆相交且过圆心 |
| B、直线与圆相交但不过圆心 |
| C、相切 |
| D、相离 |
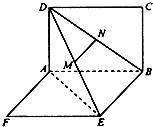 如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1.线段AB的长为
如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1.线段AB的长为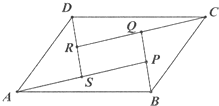 如图,在平行四边形ABCD中,设
如图,在平行四边形ABCD中,设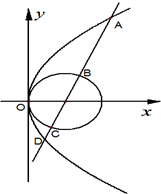 如图,抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点的直线l
如图,抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点的直线l