题目内容
已知数列an=(-1)n•n,其前n项和为Sn,则Sn= .
考点:数列的求和
专题:等差数列与等比数列
分析:当n为奇数时,Sn=-1+2-3+4-5+6-7+…+(-1)n•n=
×1-n=-
;当n为偶数时,Sn=-1+2-3+4-5+6-7+…+(-1)n•n=
×1=
.
| n-1 |
| 2 |
| n+1 |
| 2 |
| n |
| 2 |
| n |
| 2 |
解答:
解:∵数列an=(-1)n•n,其前n项和为Sn,
∴当n为奇数时,
Sn=-1+2-3+4-5+6-7+…+(-1)n•n
=
×1-n=-
;
当n为偶数时,
Sn=-1+2-3+4-5+6-7+…+(-1)n•n
=
×1=
.
∴Sn=
.
故答案为:
.
∴当n为奇数时,
Sn=-1+2-3+4-5+6-7+…+(-1)n•n
=
| n-1 |
| 2 |
| n+1 |
| 2 |
当n为偶数时,
Sn=-1+2-3+4-5+6-7+…+(-1)n•n
=
| n |
| 2 |
| n |
| 2 |
∴Sn=
|
故答案为:
|
点评:本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
相关题目
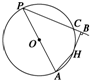 如图所示,PA为⊙O的直径,PC为⊙O的弦,过弧AC的中点H作PC的垂线交PC的延长线于点B.若HB=4,BC=2,则⊙O的直径为( )
如图所示,PA为⊙O的直径,PC为⊙O的弦,过弧AC的中点H作PC的垂线交PC的延长线于点B.若HB=4,BC=2,则⊙O的直径为( )| A、10 | B、13 | C、15 | D、20 |
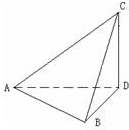 如图,将边长为1m的正△ABC沿高AD折叠成直二面角B-AD-C,则直线AC与直线AB所成角的余弦值是
如图,将边长为1m的正△ABC沿高AD折叠成直二面角B-AD-C,则直线AC与直线AB所成角的余弦值是