题目内容
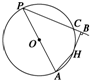如图所示，PA为⊙O的直径，PC为⊙O的弦，过弧AC的中点H作PC的垂线交PC的延长线于点B．若HB=4，BC=2，则⊙O的直径为（ ）| A、10 | B、13 | C、15 | D、20 |
考点：与圆有关的比例线段
专题：直线与圆
分析：连接CH、HA、PH，由题意知CH=HA=
=2
，由△BCH∽△PHA，得到
=
，由此能求出⊙O的直径．
| 42+22 |
| 5 |
| CH |
| PA |
| BC |
| HA |
解答：
解：连接CH、HA、PH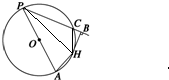
，
由题意知CH=HA=
=2
，
∵点P、A、H、C共圆，
∴∠A+∠PCH=180°，
∵∠BCH+∠PCH=180°，
∴∠BCH=∠A
∵∠CBH=∠PHA=90°
∴△BCH∽△PHA
∴
=
，
∴PA=
=
=10．
∴⊙O的直径为10．
故选：A．
，由题意知CH=HA=
| 42+22 |
| 5 |
∵点P、A、H、C共圆，
∴∠A+∠PCH=180°，
∵∠BCH+∠PCH=180°，
∴∠BCH=∠A
∵∠CBH=∠PHA=90°
∴△BCH∽△PHA
∴
| CH |
| PA |
| BC |
| HA |
∴PA=
| CH•HA |
| BC |
2
| ||||
| 2 |
∴⊙O的直径为10．
故选：A．
点评：本题考查圆的直径的求法，是中档题，解题时要认真审题，注意三角相似的性质的灵活运用．
练习册系列答案
相关题目
下列求导运算正确的是（ ）
| A、（sinx）′=-cosx | ||||
| B、（cosx）′=sinx | ||||
C、（
| ||||
| D、（2x）′=x•2x-1 |
我们把离心率为黄金比
的椭圆称之为“优美椭圆”．设F1、F2是“优美椭圆”C：
+
=1（a＞b＞0）的左、右焦点，则椭圆C上满足∠F1PF2=90°的点P的个数为（ ）
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| A、0 | B、2 |
| C、4 | D、以上答案均不正确 |
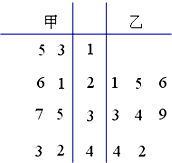以下茎叶图记录了甲、乙两名篮球运动员在以往几场比赛中得分的情况，设甲、乙两组数据的平均数分别为. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
cos75°cos105°+sin75°sin105°的值是（ ）
| A、-1 | ||||
B、-
| ||||
C、
| ||||
D、
|